题目内容
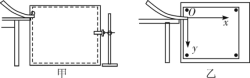
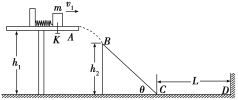
【题目】如图所示，在距地面高h1=2m的光滑水平台面上，一个质量m=1kg的小物块压缩弹簧后被锁扣K锁住，储存的弹性势能Ep=4.5J。现打开锁扣K，物块与弹簧分离后将以一定的水平速度向右滑离平台，并恰好从B点沿切线方向进入光滑的BC斜面，已知B点距水平地面的高h2=1.2m，小物块过C点无机械能损失，并与水平地面上长为L=10m的粗糙直轨道CD平滑连接，小物块沿轨道BCD运动并与右边的竖直墙壁发生碰撞，重力加速度g=10m/s2，空气阻力忽略不计。试求：
(1)小物块运动到平台末端A的瞬时速度vA大小；
(2)小物块从A到B的时间、水平位移大小以及斜面倾角θ的正切（tanθ）大小；
(3)若小物块与墙壁碰撞后速度等大反向，只会发生一次碰撞，且不能再次经过C点，那么小物块与轨道CD之间的动摩擦因数μ应该满足怎样的条件。
【答案】(1)3m/s；(2)0.4s，1.2m，
；(3)0.1225≤μ≤0.245
【解析】
(1)小物块与弹簧分离过程中，机械能守恒
EP=
解得
vA=3m/s
(2)从A到B点过程，根据平抛运动规律可知，
h1－h2=
gt2
代入数据解得
t=0.4s
水平位移
x=vAt
可得
x=1.2m
到达B点时竖直分速度为
vy=gt=4m/s
由速度的关系有
(3)依据题意有①μ的最大值对应的是物块撞墙瞬间的速度趋近于零，根据功能关系有：
mgh1＋EP>μmg
代入数据解得
μ<0.245
②对于μ的最小值求解，物体第一次碰撞后反弹，恰好不能过C点，根据功能关系有：
mgh1＋Ep≤2μmgL
解得
μ≥0.1225
综上可知满足题目条件的动摩擦因数μ值
0.1225≤μ<0.245
练习册系列答案
相关题目
