题目内容
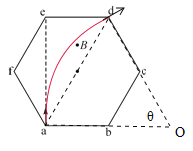
【题目】如图所示，边长为L的正六边形abcdef区域内有垂直于纸面向外的匀强磁场，磁感应强度大小为B。一质量为m、电荷量为+q（q>0）的粒子从a点沿ae方向射入磁场区域，从d点离开磁场，不计粒子重力，求粒子在磁场中运动的时间和到达d点的速度大小。
【答案】
;
【解析】
粒子在磁场中做匀速圆周运动，作出粒子运动轨迹，求出粒子做圆周运动的轨道半径，应用牛顿第二定律求出粒子的速度；根据粒子在磁场中转过的圆心角与粒子做圆周运动的周期求出粒子的运动时间．
线段ad的中垂线与直线ab的交点即为粒子做匀速圆周运动的圆心，设半径为R，由几何关系：
，
设粒子在磁场中的速度为v，洛伦兹力提供向心力：
，
联立解得：，
圆弧轨迹所对圆心角：
，
粒子在磁场中运动的时间：
，
联立解得：．
练习册系列答案
名校课堂系列答案
相关题目
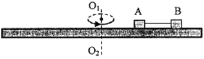
【题目】探究做功与速度变化的关系实验中，某同学利用如图所示的装置，通过数根相同的橡皮条和打点计时器，来探究橡皮条做功与小车获得速度之间的关系，得到数据如表所示，则下述说法中正确的是
A | B | C |
橡皮条数 | 速度 | 速度的平方 |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
A. 利用改变橡皮条的根数来改变做功的大小，使做功数值倍数增加
B. 每次改变橡皮条的根数，必须将小车拉到相同位置由静止释放
C. 从表格A列和B列对比，可以判断橡皮筋做功与小车速度成正比例关系
D. 从表格A列和C列对比，可以判断橡皮筋做功与小车速度平方成正比例关系
