��Ŀ����
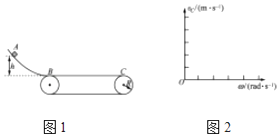
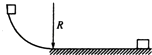
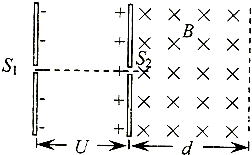
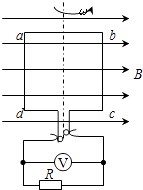
����Ŀ����ͼ��ʾΪԲ��������ĺ���森��û�дų�������£��������ӣ�������������ijһ���ٶ��ؽ���ֱ����������ʱ�������������ʱ��Ϊt����������Ӵ�ֱ���������ǿ�ų����Ÿ�Ӧǿ��ΪB��������������ͬһ���ٶ��ؽ���ֱ�����䣬�������ӷɳ�������ʱ���ٶȷ���ƫת�� ![]() ������������������õ�������Ϊ�� ��
������������������õ�������Ϊ�� ��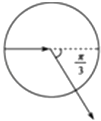
A.�������ӵıȺ�
B.�������ӵij��ٶ�
C.���������ڴų����˶��İ뾶
D.���������ڴų����˶�������
���𰸡�A,D
���������⣺�ų�ʱ����������������ֱ���˶�����Բ��������ų��İ뾶ΪR�����У�v= ![]() ����
����
���дų�ʱ����������������Բ���˶������������ṩ����������ţ�ٵڶ����ɵã�
qvB=m ![]() ����ã�����뾶��r=
����ã�����뾶��r= ![]() ����
����
�ɼ��ι�ϵ�ã�Բ�ų��뾶��Բ����뾶�Ĺ�ϵ��r= ![]() R����
R����
�ɢ٢ڢ���ʽ�ɵã� ![]() =
= ![]() ��
��
���������ڴų����˶�������Ϊ��T= ![]() =
= ![]() ��t��
��t��
���ڲ�֪Բ�ų��İ뾶����˴������ӵ��˶��뾶Ҳ�������
�Լ����ٶ����������AD��ȷ��BC����
��ѡ��AD��
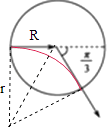
�����㾫�����������⣬������Ҫ�˽���������(��������ʼ�մ�ֱ��v�ķ���������������һ��������)����Ҫ���ո�Ӧ�����ķ���(ͨ�絼���ڴų�������������������ʹŸ��߷����йأ������ֶ���)�����֪ʶ���Ǵ���Ĺؼ���

 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�