��Ŀ����
����Ŀ����ͼ��ʾ��ƽ�а��������������ѹΪU���������ſ���С��S1��S2 �� S2�Ҳ����һ�����硢����Ϊd����ǿ�ų����ų�����ֱֽ������ų��ұ߽������������ƽ�У�����װ�ô�������У��ִ�S1������һ�����ٶ�Ϊ�㡢����Ϊm�������Ϊe�ĵ��ӣ����Ӿ��糡���ٺ��S2����ų����Ҹպ�δ�ܴӴų��ұ߽���������Ƶ�����������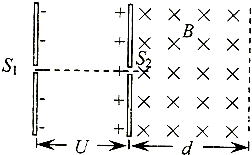
��1�����Ӿ��糡����ų�ʱ���ٶȴ�Сv��
��2����ǿ�ų��ĴŸ�Ӧǿ�ȵĴ�СB��
���𰸡�
��1��
�⣺������ƽ�а���������������ټ��ٹ��̣��ɶ��ܶ����У�
eU= ![]()
��ã�v= ![]()
��2��
�⣺�����ڴų���������Բ���˶����˶��켣ǡ��ų��ұ߽����У��ɼ��ι�ϵ�ù켣�뾶Ϊ��r=d
��ţ�ٵڶ������У�evB=m ![]()
�������ϸ�ʽ��ã�B= ![]()
����������1��������ƽ�а���������������٣��ɶ��ܶ���������ٻ�õ��ٶ�v����2���������ٶ�v����ų����ڴų������ٶ�v������Բ���˶����˶��켣ǡ��ų��ұ߽����У��ɼ��ι�ϵ��ù켣�뾶������ţ�ٵڶ����ɺ���������ʽ���B��
�����㾫����������Ҫ�����˴����������������ڵ糡�е��˶������֪ʶ�㣬��Ҫ���մ������:��Һ�Ρ��͵Ρ�������С��ȣ�����˵������ȷ�İ�ʾ���⣬һ�㶼���ܺ������������ڴ�����������ǿ�糡�����ܵ糡�����������Ǻ�������˿��������ַ�������:�������ֽⷨ;�ڵ�Ч����������������ȷ�����⣮

 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�