Question

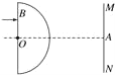
【题目】如图所示，MN为竖直放置的光屏，光屏的左侧有半径为R、折射率为的透明半球体，O为球心，轴线OA垂直于光屏，O至光屏的距离OA＝2R.一细束单色光垂直射向半球体的平面，在平面的入射点为B，OB＝R,求：

(1)光线从透明半球体射出时，出射光线偏离原方向的角度．

(2)光线在光屏形成的光斑到A点的距离．

Answer 1

【答案】(1) 30° (2) R.

【解析】

(1)分析如图．

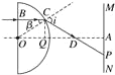
设入射点B到O的垂直距离BO＝h，∠BCO＝β，折射角为i.对OBC，由正弦公式得：

sinβ＝＝

又

n＝＝

联立解得

sini＝

所以：

i＝60°

出射光线偏离原方向的角度：

Δθ＝i－β＝60°－30°＝30°

(2)设出射光线与MN交于P点，与OA交与D点，则由几何关系可得，∠CDQ＝30°；所以：

OQ＝QD＝Rcos 30°＝R；

AD＝AO－OD＝2R－2×R＝R；

所以：

PA＝AD·tan 30°＝R×＝R.