题目内容
3.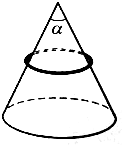 如图所示,一长L、质量均匀为M的柔软绳套在一表面光滑、顶角为α的圆锥上,当柔绳在圆锥面上静止时,柔绳中的张力是多少?
如图所示,一长L、质量均匀为M的柔软绳套在一表面光滑、顶角为α的圆锥上,当柔绳在圆锥面上静止时,柔绳中的张力是多少?
分析 取软绳中很小的一段质量元进行分析,根据受力分析可求得张力与合力的关系;再由共点力的平衡条件可明确合力与重力之间的关系;联立可求得张力T.
解答 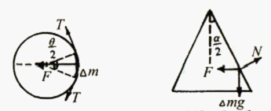 解:作出俯视图,设质量元△m两端所受张力为T,其合力为F,因为它所对的圆心角θ很小,所以sinθ等价于θ,即:
解:作出俯视图,设质量元△m两端所受张力为T,其合力为F,因为它所对的圆心角θ很小,所以sinθ等价于θ,即:
F=2Tsin($\frac{θ}{2}$)=Tθ.
再作出正视图,质量元受重力△mg、支持力N和张力的合力F而处于平衡状态,由几何知识可得:
F=△mgcot($\frac{α}{2}$)=$\frac{θ}{2π}$Mgcot($\frac{α}{2}$)
所以软绳内的张力为:
T=$\frac{F}{2}$=$\frac{mgcos(\frac{α}{2})}{2π}$
答:柔绳中的张力是为$\frac{mgcos(\frac{α}{2})}{2π}$
点评 本题采用微元法进行分析,要注意明确绳上的张力与弹力之间的关系;并能正确根据共点力的平衡进行分析求解,难度较大.

练习册系列答案
相关题目
18.Bungee(蹦极)是一种新兴的体育活动,蹦跃者站在约40米以上(相当于10层楼高)高度的桥梁、塔顶、高楼、吊车甚至热气球上,把一端固定的一根长长的橡皮条绑在踝关节处,然后两臂伸开,双腿并拢,头朝下跳下去.绑在跳跃者踝部的橡皮条很长,足以使跳跃者在空中享受几秒钟的“自由落体”.当人体落到离地面一定距离时,橡皮绳被拉开、绷紧,阻止人体继续下落,当人到达最低点时,橡皮绳再次弹起,人被拉起,随后又落下,如此反复,但由于空气阻力的原因,使弹起的高度会逐渐减小,直到静止,这就是蹦极的全过程.根据以上的叙述,忽略空气阻力的影响,对第一次下落过程中下列说法正确的是( )
| A. | 当橡皮绳达到原长后人开始做减速运动 | |
| B. | 整个下落过程中人的机械能守恒 | |
| C. | 当橡皮绳的弹力刚好等于人的重力时人的加速度最大 | |
| D. | 当人达到最低点时加速度数值最大,且一定大于重力加速度g的值 |
15. 如图所示,在超市中,小张沿水平方向推着质量为m的购物车乘着沿自动扶梯方向加速度为a匀加速上升的自动扶梯上楼.假设小张、购物车、自动扶梯间保持相对静止,自动扶梯的倾角为θ,小张的质量为M,小张与扶梯间的摩擦因数为μ,小车与扶梯间的摩擦忽略不计.则( )
如图所示,在超市中,小张沿水平方向推着质量为m的购物车乘着沿自动扶梯方向加速度为a匀加速上升的自动扶梯上楼.假设小张、购物车、自动扶梯间保持相对静止,自动扶梯的倾角为θ,小张的质量为M,小张与扶梯间的摩擦因数为μ,小车与扶梯间的摩擦忽略不计.则( )
 如图所示,在超市中,小张沿水平方向推着质量为m的购物车乘着沿自动扶梯方向加速度为a匀加速上升的自动扶梯上楼.假设小张、购物车、自动扶梯间保持相对静止,自动扶梯的倾角为θ,小张的质量为M,小张与扶梯间的摩擦因数为μ,小车与扶梯间的摩擦忽略不计.则( )
如图所示,在超市中,小张沿水平方向推着质量为m的购物车乘着沿自动扶梯方向加速度为a匀加速上升的自动扶梯上楼.假设小张、购物车、自动扶梯间保持相对静止,自动扶梯的倾角为θ,小张的质量为M,小张与扶梯间的摩擦因数为μ,小车与扶梯间的摩擦忽略不计.则( )| A. | 小张对扶梯的压力大小为Mgcosθ,方向垂直于斜面向下 | |
| B. | 小张对扶梯的摩擦力大小为(M+m)(gsin θ+a),方向沿斜面向下 | |
| C. | 扶梯对小张的摩擦力大小为μ(M+m)gcosθ,方向沿斜面向上 | |
| D. | 小张对车的推力和车对小张的弹力是一对平衡力,因为人和车处于平衡状态,所以两者大小相等 |
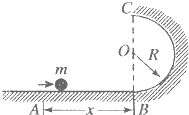 如图所示,水平直轨道末端B点处刚好与一光滑的半圆弧轨道平滑相连,C点为半圆弧轨道的顶点,圆弧半径R=30cm.现在有一质量m=3kg的小木块以某一初速度V0向右运动,并能沿圆弧轨道滑行.已知木块与水平轨道间的动摩擦因数μ=0.5,A点与B点的距离L=12m.木块通过最高点C时,木块对轨道的压力F为10N,求V0的大小?
如图所示,水平直轨道末端B点处刚好与一光滑的半圆弧轨道平滑相连,C点为半圆弧轨道的顶点,圆弧半径R=30cm.现在有一质量m=3kg的小木块以某一初速度V0向右运动,并能沿圆弧轨道滑行.已知木块与水平轨道间的动摩擦因数μ=0.5,A点与B点的距离L=12m.木块通过最高点C时,木块对轨道的压力F为10N,求V0的大小?
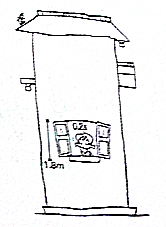 一雨滴从屋檐由静止自由下落,通过高度为h=1.8m的窗户时间为t=0.2s,求屋檐到窗台的高度H(g取10m/s2)
一雨滴从屋檐由静止自由下落,通过高度为h=1.8m的窗户时间为t=0.2s,求屋檐到窗台的高度H(g取10m/s2)
 如图所示,在真空中相距为L的A、B两点分别放置在同一水平线上,电量大小均为Q的正负点电荷,那么在离A、B两点距离都等于L的点的电场强度方向为由A指向B,该点的场强大小为$k\frac{Q}{{l}^{2}}$.?
如图所示,在真空中相距为L的A、B两点分别放置在同一水平线上,电量大小均为Q的正负点电荷,那么在离A、B两点距离都等于L的点的电场强度方向为由A指向B,该点的场强大小为$k\frac{Q}{{l}^{2}}$.?