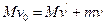题目内容
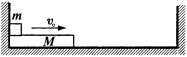
如图所示,在光滑的水平面上固定有左、右两竖直挡板,挡板间距离足够长,有一质量为M,长为L的长木板靠在左侧挡板处,另有一质量为m的小物块(可视为质点),放置在长木板的左端,已知小物块与长木板间的动摩擦因数为μ,且M>m.现使小物块和长木板以共同速度v0向右运动,设长木板与左、右挡板的碰撞中无机械能损失.试求:
(1)将要发生第二次碰撞时,若小物块仍未从长木板上落下,则它应距长木板左端多远?
(2)为使小物块不从长木板上落下,板长L应满足什
么条件?
(3)若满足(2)中条件,且M=2kg,m=1kg,v0=10m/s,试计算整个系统在刚发生第四次碰撞前损失的机械能.

(1)将要发生第二次碰撞时,若小物块仍未从长木板上落下,则它应距长木板左端多远?
(2)为使小物块不从长木板上落下,板长L应满足什
么条件?
(3)若满足(2)中条件,且M=2kg,m=1kg,v0=10m/s,试计算整个系统在刚发生第四次碰撞前损失的机械能.
(1)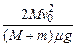 ;(2)
;(2)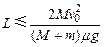 ;(3)149.8J
;(3)149.8J
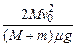 ;(2)
;(2)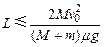 ;(3)149.8J
;(3)149.8J(1)第一次与右挡板碰后到达共同速度v1的过程中,对m、M组成的系统,选定水平向左为正方向.
由动量守恒可得(M-m)v0=(M+m)v1 ①
由能量守恒可得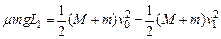 ②
②
由①②解得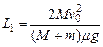
(2)上述过程中,m相对M向右滑动,且共同速度v1向左.以后,M与左挡板碰撞,碰后m相对M向左滑动,直到重新达到共同速度v2,则
(M-m)v1=(M+m)v2 ③
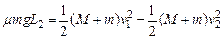 ④
④
由③④解得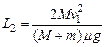
显然L2<L1,同理L3<L2,…
因此,只有第一次碰后m未从M上掉下,以后就不可能掉下,则长木板的长度L应满足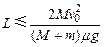
(3)根据能量守恒可得,到刚发生第四次碰撞前,系统损失的机械能
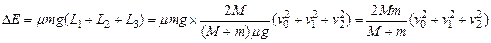 ⑤又
⑤又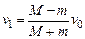 ⑥
⑥
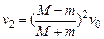 ⑦
⑦
所以,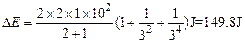
由动量守恒可得(M-m)v0=(M+m)v1 ①
由能量守恒可得
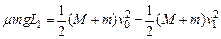 ②
②由①②解得
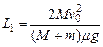
(2)上述过程中,m相对M向右滑动,且共同速度v1向左.以后,M与左挡板碰撞,碰后m相对M向左滑动,直到重新达到共同速度v2,则
(M-m)v1=(M+m)v2 ③
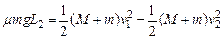 ④
④由③④解得
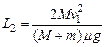
显然L2<L1,同理L3<L2,…
因此,只有第一次碰后m未从M上掉下,以后就不可能掉下,则长木板的长度L应满足
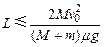
(3)根据能量守恒可得,到刚发生第四次碰撞前,系统损失的机械能
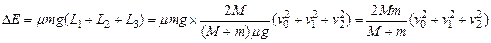 ⑤又
⑤又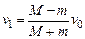 ⑥
⑥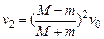 ⑦
⑦所以,
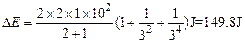

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 停放着一辆质量M=6.0kg平板车,在车上左端放有一质量mB=4.0kg木块B。车左边紧邻一个与平板车等高的光滑水平面,现有另一质量mA= 2.0kg的木块A,从左侧光滑水平面上以v0=3.0m/s向右运动,然后与B发生碰撞,设木块A、B碰撞时间很短且为弹性正碰。碰后木块B开始在平板车上滑行,并与固定在平板车上的水平轻质弹簧作用后与弹簧分离,已知木块B把弹簧压缩到最短时距离平板车左侧的距离为L=0.20m,重力加速度为g=10m/s2,木块B与平板车之间的动摩擦因数为μ=0.50。(结果保留两位有效数字)求:
停放着一辆质量M=6.0kg平板车,在车上左端放有一质量mB=4.0kg木块B。车左边紧邻一个与平板车等高的光滑水平面,现有另一质量mA= 2.0kg的木块A,从左侧光滑水平面上以v0=3.0m/s向右运动,然后与B发生碰撞,设木块A、B碰撞时间很短且为弹性正碰。碰后木块B开始在平板车上滑行,并与固定在平板车上的水平轻质弹簧作用后与弹簧分离,已知木块B把弹簧压缩到最短时距离平板车左侧的距离为L=0.20m,重力加速度为g=10m/s2,木块B与平板车之间的动摩擦因数为μ=0.50。(结果保留两位有效数字)求:

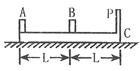
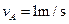 的速度向左滑行,同时滑块B以
的速度向左滑行,同时滑块B以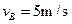 的速度向右滑行,当滑块B与P处相距
的速度向右滑行,当滑块B与P处相距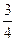 L时,二者刚好处于相对静止状态,若在二者共同运动方向的前方有一障碍物,木板A与它碰后以原速率反弹(碰后立即撤去该障碍物).求B与A的粗糙面之间的动摩擦因数
L时,二者刚好处于相对静止状态,若在二者共同运动方向的前方有一障碍物,木板A与它碰后以原速率反弹(碰后立即撤去该障碍物).求B与A的粗糙面之间的动摩擦因数 和滑块B最终停在木板A上的位置.(g取10m/s2)
和滑块B最终停在木板A上的位置.(g取10m/s2)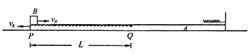

 ,2 v
,2 v
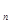 ;
; ;
;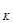
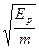 B.
B.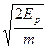 C.2
C.2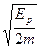
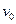 匀速行驶,从船上以相对海岸的水平速度
匀速行驶,从船上以相对海岸的水平速度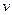 沿前进方向射出一质量为m的炮弹,发射炮弹后艇的速度为
沿前进方向射出一质量为m的炮弹,发射炮弹后艇的速度为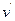 ,若不计水的阻力,则下列各关系式中正确的是 。(填选项前的编号)
,若不计水的阻力,则下列各关系式中正确的是 。(填选项前的编号) ①
①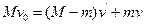 ②
② 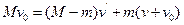
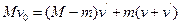 ④
④