题目内容
如图所示,一块足够长的木板,放在光滑水平面上,在木板上自左向右并非放有序号是1,2,3,…,n的物体,所有物块的质量均为m,与木板间的动摩擦因数都相同,开始时,木板静止不动,第1,2,3,…n号物块的初速度分别是v ,2 v
,2 v ,3 v
,3 v ,…nv
,…nv ,方向都向右,木板的质量与所有物块的总质量相等,最终所有物块与木板以共同速度匀速运动。设物块之间均无相互碰撞,木板足够长。试求:
,方向都向右,木板的质量与所有物块的总质量相等,最终所有物块与木板以共同速度匀速运动。设物块之间均无相互碰撞,木板足够长。试求:

小题1:所有物块与木板一起匀速运动的速度v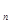 ;
;
小题2:第1号物块与木板刚好相对静止时的速度v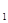 ;
;
小题3:通过分析与计算说明第k号(k<n=物块的最小速度v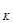
 ,2 v
,2 v ,3 v
,3 v ,…nv
,…nv ,方向都向右,木板的质量与所有物块的总质量相等,最终所有物块与木板以共同速度匀速运动。设物块之间均无相互碰撞,木板足够长。试求:
,方向都向右,木板的质量与所有物块的总质量相等,最终所有物块与木板以共同速度匀速运动。设物块之间均无相互碰撞,木板足够长。试求:
小题1:所有物块与木板一起匀速运动的速度v
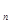 ;
;小题2:第1号物块与木板刚好相对静止时的速度v
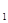 ;
;小题3:通过分析与计算说明第k号(k<n=物块的最小速度v
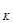
小题1:v
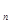 =
=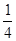 (n+1)v
(n+1)v ,
,小题2:v
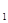 =
=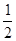 v
v
小题3:v
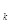 =
=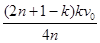
 小题1:设所有物块都相对木板静止时的速度为 v
小题1:设所有物块都相对木板静止时的速度为 v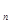 ,因木板与所有物块系统水平方向不受外力,动量守恒,应有:
,因木板与所有物块系统水平方向不受外力,动量守恒,应有:m v
 +m·2 v
+m·2 v +m·3 v
+m·3 v +…+m·n v
+…+m·n v =(M + nm)v
=(M + nm)v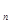 1
1M = nm, 2
解得: v
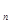 =
=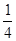 (n+1)v
(n+1)v ,
,小题2:设第1号物块相对木板静止时的速度为v
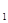 ,取木板与物块1为系统一部分,第2 号物块到第n号物块为系统另一部分,则
,取木板与物块1为系统一部分,第2 号物块到第n号物块为系统另一部分,则木板和物块1 △p =(M + m)v
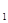 -m v
-m v ,
,2至n号物块 △p
 =(n-1)m·(v
=(n-1)m·(v - v
- v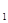 )
)由动量守恒定律:△p=△p
 ,
,解得 v
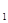 =
=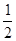 v
v , 3
, 3小题3:设第k号物块相对木板静止时的速度由v
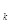 ,则第k号物块速度由k v
,则第k号物块速度由k v 减为v
减为v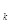 的过程中,序数在第k号物块后面的所有物块动量都减小m(k v
的过程中,序数在第k号物块后面的所有物块动量都减小m(k v - v
- v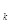 ),取木板与序号为1至K号以前的各物块为一部分,则
),取木板与序号为1至K号以前的各物块为一部分,则 △p=(M+km)v
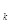 -(m v
-(m v +m·2 v
+m·2 v +…+mk v
+…+mk v )=(n+k)m v
)=(n+k)m v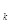 -
-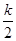 (k+1)m v
(k+1)m v
序号在第k以后的所有物块动量减少的总量为
△p
 =(n-k)m(k v
=(n-k)m(k v - v
- v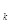 )
)由动量守恒得 △p=△p
 ,即
,即(n+k)m v
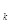 -
-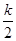 (k+1)m v
(k+1)m v = (n-k)m(k v
= (n-k)m(k v - v
- v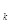 ),
),解得 v
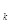 =
=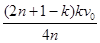

练习册系列答案
相关题目
 开始运动,并与固定在木板另一端的弹簧相碰后返回,恰好又停在木板左端,求:
开始运动,并与固定在木板另一端的弹簧相碰后返回,恰好又停在木板左端,求: