题目内容
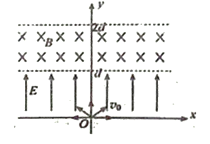
【题目】如图所示，将某正粒子放射源置于原点O，其向各方向射出的粒子速度大小均为v0、质量均为m、电荷量均为q。在0≤y≤d的一、二象限范围内分布着一个匀强电场，方向与y轴正向相同。在d<y≤2d的一、二象限范围内分布着一个匀强磁场，磁场方向垂直xoy平面向里。粒子离开电场上边缘y= d时，能够到达的最右侧的位置为(1.5d，d)， 最终恰好没有粒子从y=2d的边缘离开磁场。已知: sin30°=0.5， cos30°= 
，sin37°=0.6， cos37°=0.8， sin 45°=
，cos45°=，不计粒子重力以及粒子间的相互作用。求:
(1)电场强度E.
(2)磁感应强度B
(3)粒子在磁场中运动的最长时间.
【答案】（1）
；（2）
；（3）
【解析】
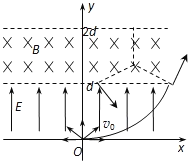
（1）沿x轴正方向发射的粒子有：x=1.5d，y=d，
由类平抛运动基本规律得：
x=v0t，
y=
at2，
而
a=
，
联立可得：
E=
（2）沿x轴正方向发射的粒子射入磁场时有：
1.5d=v0t，
d=
t，
联立可得：
，
则：
，
方向与水平成53°，斜向右上方，
据题意知该粒子轨迹恰与上边缘相切，则其余粒子均达不到y=2d边界，由几何关系可知：
d=R+
R，
根据牛顿第二定律得：
解得：
联立可得：
（3）粒子运动的最长时间对应最大的圆心角，经过(1.5d，d)恰与上边界相切的粒子轨迹对应的圆心角最大，由几何关系可知圆心角为：
θ=254°，
粒子运动周期为：
，
则时间为：
练习册系列答案
相关题目
