题目内容
20. 如图所示,水平轨道AB段长为5m,与小木块的摩擦因素μ=0.2,光滑半圆弧的半径R=0.5m,小木块的质量m=2kg,小木块原先静止在A点,在水平拉力F=12N的作用下,从A运动到B后,撤去拉力F.求
如图所示,水平轨道AB段长为5m,与小木块的摩擦因素μ=0.2,光滑半圆弧的半径R=0.5m,小木块的质量m=2kg,小木块原先静止在A点,在水平拉力F=12N的作用下,从A运动到B后,撤去拉力F.求(1)小木块到达B点时的速率;
(2)小木块对B点的压力;
(3)小木块最后在AB段的落点到B的距离.
分析 (1)研究物块在水平面上运动的过程,根据牛顿第二定律求出加速度,由速度位移关系公式求出小木块到达B点时的速率.
(2)在B点,由牛顿第二定律求出轨道对物块的支持力,再由牛顿第三定律求物块对轨道的压力.
(3)物块从B到C,运用机械能守恒定律求出物块通过C点的速度,再由平抛运动的规律求BD间的距离.
解答 解:(1)物块在水平面上运动时,由牛顿第二定律得:
F-μmg=ma
代入数据解得:a=4m/s2;
由x=$\frac{{v}^{2}-0}{2a}$得到达B点的速度:${v}_{B}=\sqrt{2ax}=\sqrt{2×4×5}=2\sqrt{10}$m/s
(2)由牛顿第二定律:N-mg=m$\frac{{v}_{B}^{2}}{R}$
代入数据解得:N=180N
由牛顿第三定律得物块对轨道的压力:N′=N=180N
(3)从B到C的过程,由机械能守恒定律得:2mgR+$\frac{1}{2}m{v}_{C}^{2}$=$\frac{1}{2}m{v}_{B}^{2}$
物块离开C点后做平抛运动,则:
2R=$\frac{1}{2}g{t}^{2}$
x=vCt
代入数据解得:${v}_{C}=2\sqrt{5}$m/s;x=2m
答:(1)小木块到达B点时的速率是$2\sqrt{10}$m/s;
(2)小木块对B点的压力是180N;
(3)小木块最后在AB段的落点到B的距离是2m.
点评 对于平抛运动的问题我们的思路是分解,从水平方向和竖直方向去研究.对于圆周运动的受力问题,关键要找出向心力的来源.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.在下列所描述的运动中,不可能存在的是( )
| A. | 速度变化很大,但加速度却很小 | |
| B. | 速度变化的方向为正,加速度方向却为负 | |
| C. | 速度变化越来越快,速度却越来越小 | |
| D. | 速度越来越大,速度变化越来越慢 |
8.一个质量为2kg的物体高度下降了2m,则重力势能减少了( )
| A. | 4J | B. | 20J | C. | 40J | D. | -40J |
15.关于电场强度的公式E=$\frac{F}{q}$和E=$\frac{kQ}{{r}^{2}}$,下列说法正确的有( )
| A. | 公式E=$\frac{F}{q}$只适用于点电荷产生的电场 | |
| B. | 公式E=$\frac{F}{q}$是定义式,E与q无关 | |
| C. | 公式E=$\frac{kQ}{{r}^{2}}$只适用于点电荷产生的电场 | |
| D. | 由公式E=$\frac{kQ}{{r}^{2}}$知,当离电荷很近时(r→0)时,电场强度E可达无穷大 |
5.某物体运动的v-t图象如图所示,则下列说法正确的是( )


| A. | 物体在第1s末运动方向发生变化 | |
| B. | 物体在第2s内和第3s内的加速度是相同的 | |
| C. | 物体在2s末返回出发点 | |
| D. | 物体在1s末离出发点最远 |
12.关于弹力,下列哪些说法是正确的( )
| A. | 两个物体一接触就会产生弹力 | |
| B. | 弹簧的弹力大小总是与弹簧的长度成正比 | |
| C. | 弹簧的弹力大小总是与弹簧的伸长量成正比 | |
| D. | 物体具有弹性形变是产生弹力的前提条件 |
10.关于物理学史,下列说法中正确的是( )
| A. | 电荷量e的数值最早是由美国物理学家密立根测得的 | |
| B. | 法拉第不仅提出了场的概念,而且直观地描绘了场的清晰图象 | |
| C. | 卡文迪许通过实验研究确认了真空中两点电荷之间相互作用力的规律 | |
| D. | 法拉第在前人工作的基础上,通过实验研究确认了真空中两个静止点电荷之间的相互作用力的规律 |
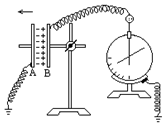 如图所示,是研究平行板电容器电容的实验装置,其中极板A接地,极板B与静电计相接,静电计外壳也接地.在实验中,若将A极板稍向左移动一些,增大电容器两极板间的距离,电容器所带的电量可视为不变,这时可观察到静电计金属箔张角会变大,两极板间电势差变大,两极板间的电场强度不变,电容变小,(填“变大”“变小”或“不变”)
如图所示,是研究平行板电容器电容的实验装置,其中极板A接地,极板B与静电计相接,静电计外壳也接地.在实验中,若将A极板稍向左移动一些,增大电容器两极板间的距离,电容器所带的电量可视为不变,这时可观察到静电计金属箔张角会变大,两极板间电势差变大,两极板间的电场强度不变,电容变小,(填“变大”“变小”或“不变”)