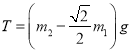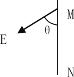题目内容
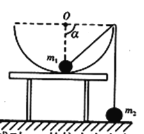
【题目】在绝缘水平面上放一质量m=2.0×10-3kg的带正电的滑块A,所带电荷量q=1.0×10-7C.在滑块A的左边l=0.3m处放置一个不带电的绝缘滑块B,质量M=4.0×10-3kg,B与一端连在竖直墙壁上的轻弹簧接触(不连接)且弹簧处于自然状态,弹簧原长S=0.05m.如图所示,在水平面上方空间加一水平向左的匀强电场,电场强度的大小为E=4.0×105N/C,滑块A由静止释放后向左滑动并与滑块B发生碰撞,设碰撞时间极短,碰撞后两滑块结合在一起共同运动并一起压缩弹簧至最短处(弹性限度内),此时弹性势能E0=3.2×10-3J,两滑块始终没有分开,两滑块的体积大小不计,与水平面间的动摩擦因数均为μ=0.5,g取10m/s2.求:(结果保留一位有效数字)
(1)两滑块碰撞后刚结合在一起的共同速度是多少?
(2) 弹簧弹被压缩过程的最短长度是多少?
(3)两滑块被弹簧弹开后距竖直墙壁的最大距离是多少?

【答案】(1) v=1.0m/s(2)0.03m(3) 0.08m
【解析】
(1)设两滑块碰前A的速度为v1,由动能定理有:
![]()
解得:
v1=3m/s
A、B两滑块碰撞,由于时间极短动量守恒,设共同速度为v
![]()
解得:
v=1.0m/s
(2)碰后A、B一起压缩弹簧至最短,设弹簧压缩量为x1,由动能定理有:
![]()
解得:
x1=0.02m
所以,弹簧弹被压缩过程的最短长度
x=S-x1=0.03m
(3)设反弹后A、B滑行了x2距离后速度减为零,由动能定理得:
![]()
解得:
x2≈0.05m
以后,因为
qE>μ(M+m)g
滑块还会向左运动,但弹开的距离将逐渐变小,所以,最大距离为:
xm=x2+s-x1=0.05m+0.05m-0.02m=0.08m.

【题目】某中学生课外科技活动小组利用铜片,锌片和橙汁制作了橙汁电池,他们用如图所示的实验电路测量这种电池的电动势E和内阻r。图中电流表的内阻为100Ω,量程为0—300mA;电阻箱阻值的变化范围为0—9999Ω。
(1)连接电路后,开关闭合前电阻箱及的阻值应调节到__________(填“最大”,“最小”,“任意值”)
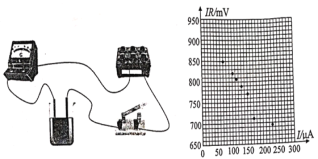
(2)闭合开关,调节电阻箱R的阻值,得到的测量数据如表格所示。请作出本实验的IR-I图象_____。
表格:电阻箱示数R和电流表的读数I
R/KΩ | 12.10 | 8.00 | 7.00 | 6.00 | 5.00 | 4.18 | 3.03 |
I/μA | 71 | 102 | 115 | 131 | 152 | 170 | 230 |
IR/mV | 850 | 816 | 805 | 786 | 760 | 716 | 696 |
(3)根据图像得出该橙汁电池的电动势为__________V,内阻为__________Ω