题目内容
乘客在地铁列车中能忍受的最大加速度是1.4m/s2,已知某两个必停站相距2240m,求:
(1)如果列车最大运行速度为28m/s,列车在这两站间的行驶时间至少是多少?
(2)假设没有最大速度限制,列车在两站间行驶的最短时间是多少?
(1)如果列车最大运行速度为28m/s,列车在这两站间的行驶时间至少是多少?
(2)假设没有最大速度限制,列车在两站间行驶的最短时间是多少?
解:(1)设列车加速到最大速度所用时间为t1,则有:v=at1,t1=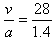 =20s
=20s
运动的位移为:x1=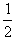 at21=
at21= ×1.4×202m=280m
×1.4×202m=280m
同理:减速过程所用时间为:t2=t1=20s
减速过程运动的位移为:x2=x1=280m
匀速运行的时间为:t3=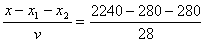 s=60s
s=60s
即两站间运行时间为:t=t1+t2+t3=100s
(2)若没有最大速度限制,列车可只有加速和减速两个过程,且两个过程位移相等,即:
x′=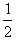 x=1120m
x=1120m
由运动学公式得:x′=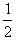 at′2
at′2
解得:t'=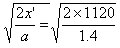 s=40s
s=40s
t=2t′=80s

练习册系列答案
相关题目