题目内容
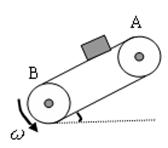
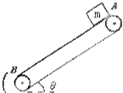如图所示，传送带与地面倾角θ=37°，从A到B长度为16m，传送带以10m/s的恒定速率针转动，在传送带上端A处无初速度放一个质量为0.5kg的小物体，它与传送带的摩擦系数为0.5，其它摩擦不计，已知sin37°=0.6，cos37°=0.8，g取10m/s2．求：（1）若传送带顺时针转动，物体由A滑到B的时间？（2）若传送带逆时针转动，物体由A滑到B的时间？
分析：（1）隔离法选取小物块为研究对象进行受力分析，然后由牛顿第二定律求小物块的加速度，然后由运动学公式求解．（2）物体在传送带上受到重力、支持力和摩擦力作用先做初速度为0的匀加速直线运动，当速度和传送带速度一样时进行判断物体跟随传送带匀速还是单独做匀变速直线运动，根据总位移为16m，可以求出整个运动过程的时间t．
解答：解：（1）若传送带顺时针转动，以小物块为研究对象，受重力为mg，受支持力为N，受摩擦力为f，
设小物块的加速度为a1，根据牛顿第二定律：mgsinθ-f=ma1…①
N-mgcosθ=0…②
f=μN..③
联立①②③代入数据解得：a1=2m/s2
小物块一直以加速度a1运动下去，根据l=
a1t2
代入数据解得：t=4s
（2）若传送带逆时针转动，物体放上传送带后，开始一段时间t1内做初速度为0的匀加速直线运动，小物体受到沿斜面向下的摩擦力：
可知，物体所受合力F合=mgsinθ+f
又因为f=μN=μmgcosθ
所以根据牛顿第二定律可得：
a=
=10m/s2
当物体速度增加到10m/s时产生的位移
x=
=5m＜16m
所用时间为：t=
=1s
所以物体速度增加到10m/s后，由于mgsinθ＞μmgcosθ，所以物体将受沿传送带向上的摩擦力直线运动，物体向下做匀加速运动．
所以物体的加速度：a2=
=2m/s2
匀加速运动的位移为16-x，设所用时间为t′，
则：16-x=11=vt′+
at′2
解得：t′=1s或-11s（舍去）
t总=1s+1s=2s
答：（1）若传送带顺时针转动，物体由A滑到B的时间为4s．（2）若传送带逆时针转动，物体从A到B需要的时间为2s．
设小物块的加速度为a1，根据牛顿第二定律：mgsinθ-f=ma1…①
N-mgcosθ=0…②
f=μN..③
联立①②③代入数据解得：a1=2m/s2
小物块一直以加速度a1运动下去，根据l=
| 1 |
| 2 |
代入数据解得：t=4s
（2）若传送带逆时针转动，物体放上传送带后，开始一段时间t1内做初速度为0的匀加速直线运动，小物体受到沿斜面向下的摩擦力：
可知，物体所受合力F合=mgsinθ+f
又因为f=μN=μmgcosθ
所以根据牛顿第二定律可得：
a=
| F合 |
| m |
当物体速度增加到10m/s时产生的位移
x=
| v2 |
| 2a |
所用时间为：t=
| v |
| a |
所以物体速度增加到10m/s后，由于mgsinθ＞μmgcosθ，所以物体将受沿传送带向上的摩擦力直线运动，物体向下做匀加速运动．
所以物体的加速度：a2=
| mgsinθ- μmgcosθ |
| m |
匀加速运动的位移为16-x，设所用时间为t′，
则：16-x=11=vt′+
| 1 |
| 2 |
解得：t′=1s或-11s（舍去）
t总=1s+1s=2s
答：（1）若传送带顺时针转动，物体由A滑到B的时间为4s．（2）若传送带逆时针转动，物体从A到B需要的时间为2s．
点评：解决本题的关键理清物体的运动规律，知道物体运动，明确速度和加速度的变化，结合牛顿第二定律和运动学公式进行求解．从此题看出出，皮带传送物体所受摩擦力可能发生突变，不论是其大小的突变，还是其方向的突变，都发生在物体的速度与传送带速度相等的时刻．
练习册系列答案
相关题目
如图所示，传送带与地面的倾角θ，传送带以v匀速运动，在传送带底端无初速地放置一个质量为m的物体，当物体上升高度h时，物体已经相对传动带静止，在这个过程中分析正确的是（ ）
如图所示，传送带与地面的倾角θ=37°，从A端到B端的长度为29m，传送带以v0=10m/s的速度沿逆时针方向转动．在传送带上端A处无初速地放置一个质量为0.5kg的物体，它与传送带之间的动摩擦因数为μ=0.5，求物体从A端运动到B端所需的时间是多少？（sin37°=0.6，cos37°=0.8）
