题目内容
【题目】图甲为验证牛顿第二定律的实验装置示意图.图中打点计时器打点的时间间隔用Δt表示.在小车质量未知的情况下,某同学设计了一种方法用来探究“在外力一定的条件下,物体的加速度与其质量间的关系”.
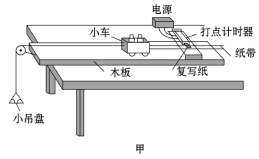
(1)实验步骤:
①平衡小车所受的阻力:先拿下小吊盘,调整木板右端的高度,用手轻拨小车,直到打点计时器打出一系列均匀的点.
②按住小车,挂上带有适当重物的小吊盘,在小车中放入砝码.
③接通打点计时器电源,释放小车,获得带有点列的纸带,在纸带上标出小车中砝码质量m.
④按住小车,改变小车中砝码的质量,重复步骤③.
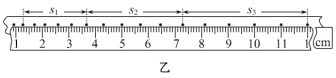
⑤在每条纸带上清晰的部分,每5个间隔标注一个计数点.测量相邻计数点的间距s1,s2……求出与不同m相对应的加速度a.
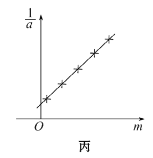
⑥以砝码的质量m为横坐标,![]() 为纵坐标,在坐标纸上作出
为纵坐标,在坐标纸上作出![]() 关系图线.
关系图线.
(2)完成下列填空:
①本实验中,为了保证在改变小车中砝码的质量时,小车所受的拉力近似不变,小吊盘和盘中物块的质量之和应满足的条件是______________________________.
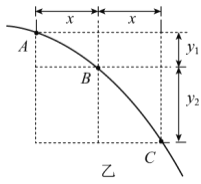
②某纸带上三个相邻计数点的间距为s1、s2和s3.则小车加速度a=__________________(用字母s1、s3和Δt表示)
③图丙为所得实验图线的示意图.设图中直线的斜率为k,在纵轴上截距为b,若牛顿定律成立,则小车受到的拉力为_______,小车的质量为_______
【答案】小吊盘和盘中物块的质量之和远小于小车和砝码的总质量 ![]()
![]()
![]()
【解析】
①[1]设小车的质量为M,小吊盘和盘中物块的质量为m,设绳子上拉力为F,以整体为研究对象有:
![]()
解得
![]()
以小车为研究对象,则有:
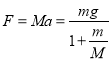
当![]() 时有
时有![]() ,即只有
,即只有![]() 时才可以认为绳对小车的拉力大小等于小吊盘和盘中物块的重力;
时才可以认为绳对小车的拉力大小等于小吊盘和盘中物块的重力;
②[2]根据
![]()
可得:
![]()
又T=5△t,解得:
![]()
③[3][4]设小车质量为M,小车受到外力为F,由牛顿第二定律有:
![]()
变形得:
![]()
则![]() 图象的斜率为
图象的斜率为
![]()
则有:
![]()
纵轴截距为
![]()
解得:
![]()

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案