题目内容
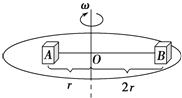
【题目】如图所示,一个光滑的圆锥体固定在水平桌面上,其轴线沿竖直方向,母线与轴线的夹角θ=30°,一条长为l的绳,一端固定在圆锥体的顶点O,另一端系一个质量为m的小球(视作质点),小球以速率v绕圆锥体的轴线做水平匀速圆周运动,则
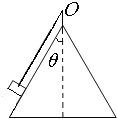
(1)当![]() 时,绳对小球的拉力多大?
时,绳对小球的拉力多大?
(2)当![]() 时,绳对小球的拉力多大?
时,绳对小球的拉力多大?
【答案】(1)![]() (2) T=2mg
(2) T=2mg
【解析】试题分析:如图(甲)所示,小球在锥面上运动,锥面对小球恰好无压力时,重力mg和绳的拉力FT提供向心力,根据牛顿第二定律得mgtan30°=![]()
解得v0=![]()
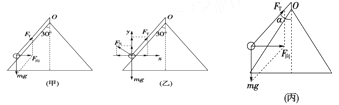
(1)因v1<v0,所以此时小球与锥面接触并产生弹力FN,受力情况如图(乙)所示,则
FTsin30°-FNcos30°=
FTcos30°+FNsin30°=mg
联立解得FT=1.03mg。
(2)因v2>v0,所以此时小球与锥面脱离,设绳与轴线的夹角为α,小球受力如图(丙)所示,则
FTsinα=![]() FTcosα=mg 联立解得FT=2mg
FTcosα=mg 联立解得FT=2mg

练习册系列答案
相关题目