题目内容
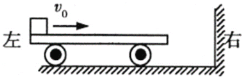
【题目】如图所示,一质量为M的平板车左端放有质量为m的滑块(已知m>M),滑块与平板车之间的动摩擦因数μ,开始时,平板车和滑块共同以速度v0沿光滑水平面向右运动,并与竖直墙壁发生弹性碰撞,设碰撞时间极短。碰后平板车原速反弹,滑块不会滑出平板车右端,重力加速度为g,求:
(1)平板车第一次与墙壁碰撞后到再次与滑块速度相同时,两者共同的速度;
(2)要使滑块不滑离平板车,平板车至少多长;
(3)试判断每次平板车与墙壁碰撞前,滑块与平板车之间是否达到相同的速度;
(4)计算从第一次长木板与挡板碰撞后开始计时,到滑块停止运动的过程中,滑块运动的总路程。
【答案】(1)![]() (2)
(2)![]() (3)已达到相同的速度;(4)
(3)已达到相同的速度;(4)![]()
【解析】
(1)平板车与墙发生碰撞后以原速率弹回,此后平板车与木块所受的合外力为零,总动量守恒,取水平向右为正方向,则有
![]()
解得
![]()
(2)当每次与墙壁碰撞后,木块都在木板上滑动,从而消耗能量,最终木块与木板的整体将停止在墙壁附近,由能量关系可知:
![]()
解得:
![]()
(3)设木块与小车与墙壁碰前的共同速度为v1,则小车与墙壁碰撞后,小车以v1速度反弹,做减速运动到零,然后反向向右加速到与木块共速v2,则v2<v1;过程中小车的加速度相同,
则小车向左减速到零的位移大于向右到共速时的位移,可知当小车与木块共速前时,小车不会碰到墙壁,即每次平板车与墙壁碰撞前,滑块与平板车之间应已经达到相同的速度。
(4)从第一次与墙壁碰撞到第二次碰撞时,木块的位移满足:
![]()
同理从第二次与墙壁碰撞到第三次碰撞时,木块的位移满足:
![]()
同理从第三次与墙壁碰撞到第四次碰撞时,木块的位移满足:
![]()
…….
小车和木板最终的速度为零,则多个式子两边相加可得:
![]()
解得
![]()

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目