题目内容
一人站在静止于光滑平直轨道的平板车上,人和车的总质量为M,现在让这人双手各握一个质量均为m的铅球,以两种方式顺着轨道方向水平投出铅球:第一次是一个一个地投;第二次是两个一起投,设每次投掷时铅球对车的速度相同,则两次投掷铅球后小车速度之比为
[ ]
A.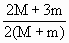
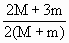
B.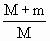
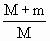
C.1
D.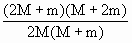
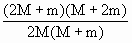
答案:A
解析:
提示:
解析:
|
巧解分析:人、铅球、车组成的系统所受的合外力为零,满足动量守恒定律. 设投铅球时球相对车的速度为v0,选车的运动方向为正方向,第一次一个一个投掷时,有两个作用过程,投掷第一个球时应有:0=(M+m)v-m(v0-v), ① 投掷第二个球时应有:(M+m)v=Mv1-m(v0-v1), ② 由①②式解得:v1=(2M+3m)mv0/(M+m)(M+2m). 第二次两个铅球一起投出时应有:0=Mv2-2m(v0-v2),解得:v2=2mv0/(M+2m). 所以两次投掷铅球后小车的速度之比:v1/v2=(2M+3m)/2(M+m).本题正确选项为A. |
提示:
|
命题意图:本题考查系统的动量守恒问题. |

练习册系列答案
相关题目