题目内容
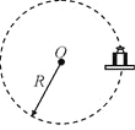
【题目】一水平放置的木板上放有砝码，砝码与木板间的动摩擦因数为μ，如果让木板在竖直平面内做半径为R的匀速圆周运动，假如运动中木板始终保持水平，砝码始终没有离开木板，且砝码与木板间的最大静摩擦力等于滑动摩擦力,那么下列说法正确的是( )
A. 在通过轨道最高点时，由于砝码处于失重状态，所以木板给砝码的支持力大于物体的重力
B. 在经过轨道最低点时，砝码对木板的压力最大，所以物体所受摩擦力最大
C. 匀速圆周运动的速率不超过
D. 在通过轨道最低点时，砝码处于失重状态，所以木板给砝码的支持力大于砝码的重力
【答案】C
【解析】
A．在通过轨道最高点时，向心加速度竖直向下，是失重，木板给砝码的支持力小于物体的重力，故A错误；
B．在最低点，向心加速度竖直向上，砝码对木板的压力最大，此时水平方向上没有力，所以摩擦力为零，故B错误；
C．木板和砝码在竖直平面内做匀速圆周运动，则所受合外力提供向心力，砝码受到重力G，木板支持力FN和静摩擦力Ff，由于重力G和支持力FN在竖直方向上，因此只有当砝所需向心力在水平方向上时静摩擦力有最大值，此位置是当木板和砝码运动到与圆心在同一水平面上时的位置，最大静摩擦力必须大于或等于砝码所需的向心力，即
，解得：
所以匀速圆周运动的速率不超过
，故C正确；
D．在通过轨道最低点时，向心加速度向上砝码处于超重状态，所以木板给砝码的支持力大于砝码的重力，故D错误；
练习册系列答案
相关题目
