Question

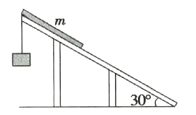
【题目】如图所示，某同学在冰面上进行“滑车”练习，开始该同学站在A车前端以共同速度v0=9m/s做匀速直线运动，在A车正前方有一辆静止的B车，为了避免两车相撞，在A车接近B车时，该同学迅速从A车跳上B车，立即又从B车跳回A车，此时A、B两车恰好不相撞，已知人的质量m=25kg，A车和B车质量均为mA=mB=100kg，若该同学跳离A车与跳离B车时对地速度的大小相等、方向相反，不计一切摩擦.则下列说法正确的是

A.该同学跳离A车和B车时对地速度的大小为10m/s

B.该同学第一次跳离A过程中对A冲量的大小为250kgm/s

C.该同学跳离B车的过程中，对B车所做的功为1050J

D.该同学跳回A车后，他和A车的共同速度为5m/s

Answer 1

【答案】ACD

【解析】

AD.由动量守恒定律可得，人对地以速度v跳离A车，

（m + mA）v0= mv+ mAvA，

人跳上 B车后共同速度为vB，

mv=（m +mB）vB；

人跳离 B车后B车对地速度为v′B，

（m +mB）vB=mBv′B -mv；

人再跳回A车后，人和A车的共同速度为v′A，

mAvA-mv =（m + mA）v′A；

两车不相撞满足：

v′A=v′B；

联立解得：

v=10 m/s，vA=m/s，vB=2 m/s，v′A= v′B= 5 m/s，

故A项正确，D项正确；

B.由动量定理可知，该同学第一次跳离A车过程中，对A 车冲量大小为：

I==25 kgm/s，

故B项错误；

C.由动能定理可知该同学跳离B车过程中对B所做的功为：

W =-=1050 J，

故C项正确。