题目内容
如图是某缓冲装置，劲度系数足够大的轻质弹簧与直杆相连，直杆可在固定的槽内移动，与槽间的滑动摩擦力恒为f，直杆质量不可忽略。一质量为m的小车以速度v0撞击弹簧，最终以速度v弹回。直杆足够长，且直杆与槽间的最大静摩擦力等于滑动摩擦力，不计小车与地面的摩擦。则( )
| A．小车被弹回时速度v一定小于v0 |
B．直杆在槽内移动的距离等于 |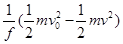
| C．直杆在槽内向右运动时，小车与直杆始终保持相对静止 |
| D．弹簧的弹力可能大于直杆与槽间的最大静摩擦力 |
BD
解析试题分析：在小车向右运动的过程中将受到弹簧向左的弹力作用做加速度逐渐增大的减速运动，若小车撞击弹簧时的速度v0较小，弹簧上的弹力小于f，小车速度即减为零，随后被弹簧，此过程中只有动能与弹性势能之间相互转化，因此最终弹回的速度v等于v0，故选项A错误；若小车撞击弹簧时的速度v0较大，在其速度还未减为零，弹簧上的弹力已增至f，由于直杆的质量不可忽略，所以小车继续做加速度增大的减速运动，弹簧继续被压缩，弹力大于f后，直杆向右做加速运动，当两者速度相等时，弹簧被压缩至最短，故选项C错误；选项D正确；当小车速度减为零时，小车反向被弹簧，弹簧弹力减小，直杆最终也不再在槽内移动，因此根据功能关系有：fx＝
－
，即直杆在槽内移动的距离为：x＝
(－)，故选项B正确。
考点：本题主要考查了牛顿第二定律、功能关系的应用问题，属于较难题。
如图所示，空间有一垂直纸面向外的磁感应强度为0.5T的匀强磁场，一质量为0.2kg且足 够长的绝缘木板静止在光滑水平面上，在木板左端无初速放置一质量为0.1kg、电荷量q=+0.2C的滑块，滑块与绝缘木板之间动摩擦因数为0.5，滑块受到的最大静摩擦力可认为等于滑动摩擦力。现对木板施加方向水平向左，大小为0.6N的恒力，g取10m/s2。则（ ） 
| A．木板和滑块一直做加速度为2m/s2的匀加速运动 |
| B．滑块开始做匀加速直线运动，然后做加速度减小的变加速运动，最后做匀速运动 |
| C．最终木板做加速度为2m/s2的匀加速运动，滑块做速度为10m/s的匀速运动 |
| D．最终木板做加速度为3m/s2的匀加速运动，滑块做速度为10m/s的匀速运动 |
如图所示，小车的质量为M，人的质量为m，人用恒力F拉绳，若人与车保持相对静止，且地面为光滑的，又不计滑轮与绳的质量，则车对人的摩擦力可能是： 
A． ，方向向左 | B．，方向向右 |
C． ，方向向右 | D． ，方向向右 |
一个质量为2kg的物体，在10个共点力作用下做匀速直线运动。现突然同时撤去大小分别为10N、12N和14N的三个力，其余的力大小方向均保持不变，关于此后该物体运动的说法中正确的是（ ）
| A．可能做匀变速曲线运动，加速度大小可能是5m/s2 |
| B．可能做匀速圆周运动，向心加速度大小5m/s2 |
| C．可能做匀减速直线运动，加速度大小是20m/s2 |
| D．一定做匀变速直线运动，加速度大小可能是10m/s2 |
质量为m的物体，在距地面h高处以
的加速度由静止竖直下落到地面。下列说法中正确的是（ ）
A．物体的重力势能减少 mgh |
| B．物体的动能增加mgh |
| C．物体的机械能减少mgh |
| D．重力做功mgh |
如图所示，离地H高处有一个质量为m、带电量为+q的物体处于电场强度随时间变化规律为
（
、
均为大于零的常数，电场水平向左为正方向）的电场中，物体与竖直绝缘墙壁间的动摩擦因数为
，已知
。
时，物体从墙上静止释放，若物体所受的最大静摩擦力等于滑动摩擦力，当物体下滑
后脱离墙面，此时速度大小为
，最终落在地面上。则下列关于物体的运动说法正确的是：
| A．当物体沿墙壁下滑时，物体先加速再做匀速直线运动 |
| B．物体从脱离墙壁到落地之前的运动轨迹是一段直线 |
C．物体克服摩擦力所做的功 |
D．物体与墙壁脱离的时刻为 |
对牛顿第二定律的理解，正确的是
| A．如果一个物体同时受到两个力的作用，则这两个力各自产生的加速度互不影响 |
| B．如果一个物体同时受到几个力的作用，则这个物体的加速度等于所受各力单独作用在物体上时产生加速度的矢量和 |
| C．平抛运动中竖直方向的重力不影响水平方向的匀速运动 |
| D．物体的质量与物体所受的合力成正比，与物体的加速度成反比 |
