题目内容
如图所示,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态,现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为a1、a2,重力加速度大小为g,则有( )
A.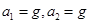 | B.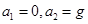 |
C.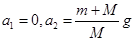 | D.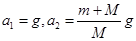 |
C
解析试题分析:静止时,木板对木块2的支持力为(M+m)g,撤去木板的瞬时,因为弹簧的弹力不能突变,所以木块1的受力情况不变,则a1=0,木板2受的合外力为(M+m)g,加速度大小为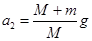 。选项C正确。
。选项C正确。
考点:牛顿定律的应用;瞬时态问题。

如图甲所示,平行于斜面的轻弹簧,劲度系数为 k,一端固定在在倾角为θ的斜面底端,另一端与Q物块连接,P、Q质量均为m,斜面光滑且固定在水平面上,初始时物块均静止.现用平行于斜面向上的力F拉物块P,使P做加速度为a 的匀加速运动,两个物块在开始一段时间内的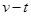 图象如图乙所示(重力加速度为g),则下列说法不正确的是( )
图象如图乙所示(重力加速度为g),则下列说法不正确的是( )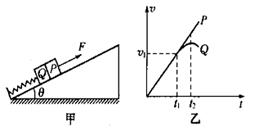
| A.平行于斜面向上的拉力F一直增大 |
| B.外力施加的瞬间,P、Q间的弹力大小为m(gsinθ—a) |
C.从O开始到t1时刻,弹簧释放的弹性势能为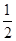 mv12 mv12 |
| D.t2时刻弹簧恢复到原长,物块Q达到速度最大值 |
某研究性学习小组用加速度传感器探究物体从静止开始做直线运动的规律,得到了质量为1.0kg的物体运动的加速度随时间变化的关系图线,如图所示。由图可以得出( )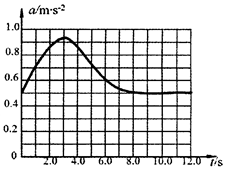
| A.从t=4.0s到t=6.0s的时间内物体做匀减速直线运动 |
| B.物体在t=10.0s时的速度大小约为5.8m/s |
| C.从t=10.0s到t=12.0s的时间内合外力对物体做的功约为7.3J |
| D.不能从已知信息粗略估算出物体在t=3.0s时的速度 |
如图所示,离地H高处有一个质量为m、带电量为+q的物体处于电场强度随时间变化规律为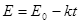 (
(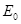 、
、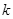 均为大于零的常数,电场水平向左为正方向)的电场中,物体与竖直绝缘墙壁间的动摩擦因数为
均为大于零的常数,电场水平向左为正方向)的电场中,物体与竖直绝缘墙壁间的动摩擦因数为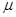 ,已知
,已知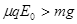 。
。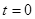 时,物体从墙上静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,当物体下滑
时,物体从墙上静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,当物体下滑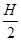 后脱离墙面,此时速度大小为
后脱离墙面,此时速度大小为 ,最终落在地面上。则下列关于物体的运动说法正确的是( )
,最终落在地面上。则下列关于物体的运动说法正确的是( )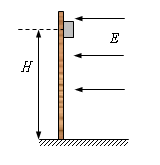
| A.当物体沿墙壁下滑时,物体先加速再做匀速直线运动 |
| B.物体从脱离墙壁到落地之前的运动轨迹是一段直线 |
C.物体客服摩擦力所做的功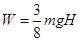 |
D.物体与墙壁脱离的时刻为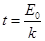 |
如图所示,用力F推放在光滑水平面上的物体P、Q、R,使其做匀加速运动. 若P和Q之间的相互作用力为6 N,Q和R之间的相互作用力为4 N,Q的质量是2 kg,那么R的质量是( )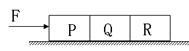
| A.2 kg | B.3 kg | C.4 kg | D.5 kg |
“飞车走壁”是一种传统的杂技艺术,演员骑车在倾角很大的桶面上做圆周运动而不掉下来.如图所示,已知桶壁的倾角为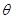 ,车和人的总质量为
,车和人的总质量为 ,做圆周运动的半径为
,做圆周运动的半径为 ,若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )
,若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )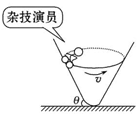
A.桶面对车的弹力为 |
B.桶面对车的弹力为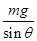 |
C.人和车的速度为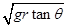 |
D.人和车的速度为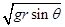 |
竖直放置在水平面上的轻质弹簧上放着质量为2kg的物体A,处于静止状态。若将一个质量为3kg的物体B竖直向下轻放在A上的一瞬间,则A与B之间的作用力大小为( )
(取g=10m/s2)
| A.30N | B.0 | C.15N | D.12N |
如图是某缓冲装置,劲度系数足够大的轻质弹簧与直杆相连,直杆可在固定的槽内移动,与槽间的滑动摩擦力恒为f,直杆质量不可忽略。一质量为m的小车以速度v0撞击弹簧,最终以速度v弹回。直杆足够长,且直杆与槽间的最大静摩擦力等于滑动摩擦力,不计小车与地面的摩擦。则( )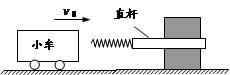
| A.小车被弹回时速度v一定小于v0 |
B.直杆在槽内移动的距离等于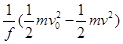 |
| C.直杆在槽内向右运动时,小车与直杆始终保持相对静止 |
| D.弹簧的弹力可能大于直杆与槽间的最大静摩擦力 |
