题目内容
太空中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其它星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个顶点上。并沿外接于等边三角形的圆形轨道运行,如图所示。设这三个星体的质量均为M,且两种系统的运动周期相同,则( )

A.直线三星系统运动的线速度大小为v= |
B.此三星系统的运动周期为T= |
C.三角形三星系统的线速度大小为v= |
D.三角形三星系统中星体间的距离为L= |
BD
解析试题分析:它们做圆周运动的向心力有彼此间的万有引力提供,对直线三星系统中做圆周运动的星,根据万有引力定律和牛顿第二定律有: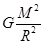 +
+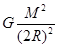 =
=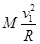 ,解得:v1=
,解得:v1= ,故选项A错误;根据匀速圆周运动参量间的关系有:T=
,故选项A错误;根据匀速圆周运动参量间的关系有:T= =
= ,故选项B正确;同理,对三角形三星系统中做圆周运动的星,有:
,故选项B正确;同理,对三角形三星系统中做圆周运动的星,有: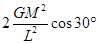 =
=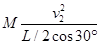 ,解得:v2=
,解得:v2=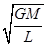 ,由于
,由于 =
=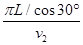 ,解得:L=
,解得:L= ,故选项D正确;显然选项C错误。
,故选项D正确;显然选项C错误。
考点:本题主要考查了圆周运动向心力、牛顿第二定律、万有引力定律的应用问题,属于中档题。

 名校课堂系列答案
名校课堂系列答案如图所示,劲度系数为k的轻弹簧竖直固定在水平面上,上端固定一质量为m0的托盘,托盘上有一个质量为m的木块。用竖直向下的力将原长为Lo的弹簧压缩后突然撤去外力,则物体m即将脱离m0时的弹簧长度为 ( )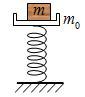
| A.Lo | B.Lo-(m0+m)g/k |
| C.Lo-mg/k | D.Lo-m0g/k |
如图所示是某公园设计的一种惊险刺激的娱乐设施. 管道除 点右侧水平部分粗糙外,其余部分均光滑. 若挑战者自斜管上足够高的位置滑下,将无能量损失的连续滑入第一个、第二个圆管形管道
点右侧水平部分粗糙外,其余部分均光滑. 若挑战者自斜管上足够高的位置滑下,将无能量损失的连续滑入第一个、第二个圆管形管道 、
、 内部(圆管
内部(圆管 比圆管
比圆管 高).某次一挑战者自斜管上某处滑下,经过第一个圆管形管道
高).某次一挑战者自斜管上某处滑下,经过第一个圆管形管道 内部最高位置时,对管壁恰好无压力.则这名挑战者
内部最高位置时,对管壁恰好无压力.则这名挑战者
A.经过管道 最高点时的机械能大于经过管道 最高点时的机械能大于经过管道 最低点时的机械能 最低点时的机械能 |
B.经过管道 最高点时的动能大于经过管道 最高点时的动能大于经过管道 最低点时的动能 最低点时的动能 |
C.经过管道 最高点时对管外侧壁有压力 最高点时对管外侧壁有压力 |
D.不能经过管道 的最高点 的最高点 |
如图所示,质量为m的物块,沿着半径为R的半球形金属壳内壁滑下,半球形金属壳竖直固定放置,开口向上,滑到最低点时速度大小为v,若物体与球壳之间的摩擦因数为μ,则物体在最低点时,下列说法正确的是( )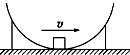
A.受到向心力为mg+m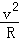 |
B.受到的摩擦力为μm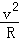 |
C.受到的摩擦力为μ(mg+m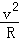 ) ) |
| D.受到的合力方向斜向左上方 |
如图 (a)所示,用一水平外力F推物体,使其静止在倾角为θ的光滑斜面上。逐渐增大F,物体开始做变加速运动,其加速度a随F变化的图象如图(b)所示。取g=10m/s2。根据图(b)中所提供的信息不能计算出的是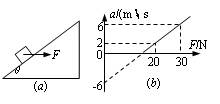
| A.物体的质量 |
| B.斜面的倾角 |
| C.使物体静止在斜面上时水平外力F的大小 |
| D.加速度为6 m/s2时物体的速度 |
Bungee(蹦极)是一种新兴的体育活动,蹦跃者站在约40m以上(相当于10层楼高)高度的桥梁、塔顶、高楼、吊车甚至热气球上,把一端固定的一根长长的橡皮条绑在踝关节处,然后两两臂伸开,双腿并拢,头朝下跳下去.绑在跳跃者踝部的橡皮条很长,足以使跳跃者在空中享受几秒钟的“自由落体”.当人体落到离地面一定距离时,橡皮绳被拉开、绷紧,阻止人体继续下落,当人到达最低点时,橡皮绳再次弹起,人被拉起,随后又落下,如此反复,但由于空气阻力的原因,使弹起的高度会逐渐减小,直到静止.这就是蹦极的全过程.根据以上的叙述,忽略空气阻力的影响,对第一次下落过程中下列说法正确的是( )
| A.当橡皮绳达到原长后人开始做减速运动 |
| B.整个下落过程中人的机械能守恒 |
| C.当橡皮绳的弹力刚好等于人的重力时人的速度最大 |
| D.当人达到最低点时加速度数值最大,且一定大于重力加速度g的值 |
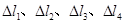 依次表示弹簧在四种情况下的伸长量,则有( )
依次表示弹簧在四种情况下的伸长量,则有( )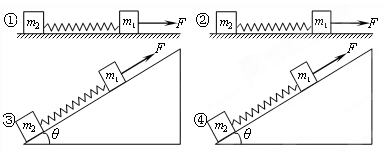
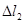 >
>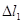
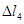 >
>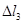



 和0
和0