题目内容
如图所示，质量分别为mA和mB的A、B两小球分别连在轻质弹簧两端，B球另一端用细线固定在倾角为30°光滑斜面上，在线被剪断瞬间，A、B两球的加速度大小分别为 ( )
A.都等于
B.和0
C．
和0
D．0和
D
解析试题分析：初始状态，两个小球和弹簧以及细线组成的整体保持静止状态，分析A球受力，弹簧拉力与A球重力沿着斜面的分力相平衡即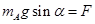
，所以弹簧弹力
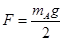，由A、B球整体平衡，设细线的拉力为T，
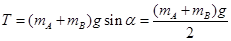。当球B连接的细线被剪断的瞬间，系统还没有运动，因此弹簧的拉力不变，因此A的受力情况未变化，于是A球瞬间仍处于平衡状，故A球的加速度为0；绳剪断瞬间B球所受的细线拉力变为0，弹簧弹力没变，则对B球根据牛顿第二定律有：
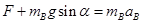,解得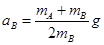
,所以D选项正确。
考点：牛顿第二定律的瞬时性应用
太空中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统，通常可忽略其它星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式：一种是三颗星位于同一直线上，两颗星围绕中央星在同一半径为R的圆轨道上运行；另一种形式是三颗星位于等边三角形的三个顶点上。并沿外接于等边三角形的圆形轨道运行，如图所示。设这三个星体的质量均为M，且两种系统的运动周期相同，则( )
A．直线三星系统运动的线速度大小为v＝ |
B．此三星系统的运动周期为T＝ |
C．三角形三星系统的线速度大小为v＝ |
D．三角形三星系统中星体间的距离为L＝ |
如图所示，足够长的U形光滑金属导轨平面与水平面成
角（
），其中MN与PQ平行且间距为L，导轨平面与磁感应强度为B的匀强磁场垂直，导轨电阻不计,NQ间接有一个阻值为R的电阻．金属棒ab由静止开始沿导轨下滑，并与两导轨始终保持垂直且良好接触，ab棒接入电路的电阻为r，当流过ab棒某一横截面的电量为q时，棒的速度大小为
，则金属棒ab在这一过程中（ ）
A．加速度大小为 |
B．下滑位移大小为 |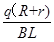
C．产生的焦耳热为 |
D．受到的最大安培力大小为 |
如图，质量为m的小球与轻质弹簧Ⅰ和水平轻绳Ⅱ相连，Ⅰ、Ⅱ的另一端分别固定于P、Q，当剪断Ⅱ的瞬间，小球的加速度a应是
| A．大小a=g |
B．大小a="g" tan |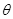
| C．方向水平向左 |
| D．方向竖直向下 |
如图所示，在光滑平面上有一静止小车，小车上静止地放置着一小物块，物块和小车间的动摩擦因数为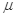
＝0.3，用水平恒力F拉动小车，下列关于物块的加速度
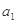和小车的加速度
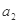。当水平恒力F取不同值时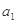，与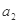的值可能为（当地重力加速度g取
）
A． ， |
B． ， |
C． ， |
D．， |
将一单摆向左拉至水平标志线上，从静止释放，当摆球运动到最低点时，摆线碰到障碍物，摆球继续向右摆动。用频闪照相机拍到如图所示的单摆运动过程的频闪照片，以下说法正确的是
| A．摆线碰到障碍物前后的周期之比为3:2． |
| B．摆线碰到障碍物前后的摆长之比为3：2 |
| C．摆球经过最低点时，线速度变小，半径减小，摆线张力变大 |
| D．摆球经过最低点时，角速度变大，半径减小，摆线张力不变 |