题目内容
17.美国科学家宣布,他们发现了可能成为太阳系第十大行星的以女神“赛德娜”命名的红色天体.如果把该行星的轨道近似为圆轨道,则它绕太阳公转的轨道半径约为地球绕太阳公转轨道半径的470倍,这是迄今为止发现的离太阳最远的太阳系行星.该天体半径约为1000km,约为地球半径的1/6.由此可以估算出它绕太阳公转的周期最接近( )| A. | 10年 | B. | 100 年 | C. | 103年 | D. | 104年 |
分析 根据万有引力提供向心力得出该天体周期与地球周期的关系,从而求出它绕太阳公转的周期.
解答 解:根据$G\frac{Mm}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$得,$T=\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$,因为轨道半径之比为470:1,则周期之比大约为104:1,因为地球的公转周期为1年,可知它绕太阳公转的周期最接近104年.故D正确,A、B、C错误.
故选:D.
点评 解决本题的关键能够获取有用信息,掌握万有引力提供向心力这一重要理论,并能灵活运用.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
13. 如图所示,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO?的距离为l,b与转轴OO?的距离为2l,木块与圆盘的最大静摩擦力为木块重力的k倍,重力加速度大小为g,使圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
如图所示,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO?的距离为l,b与转轴OO?的距离为2l,木块与圆盘的最大静摩擦力为木块重力的k倍,重力加速度大小为g,使圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
 如图所示,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO?的距离为l,b与转轴OO?的距离为2l,木块与圆盘的最大静摩擦力为木块重力的k倍,重力加速度大小为g,使圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
如图所示,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO?的距离为l,b与转轴OO?的距离为2l,木块与圆盘的最大静摩擦力为木块重力的k倍,重力加速度大小为g,使圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )| A. | b一定比a先开始滑动 | |
| B. | a、b所受的静摩擦力大小始终相等 | |
| C. | 当ω=$\sqrt{\frac{2kg}{3l}}$时,a所受摩擦力的大小为kmg | |
| D. | ω=$\sqrt{\frac{kg}{2l}}$时b开始滑动 |
14.如图所示,在孩子与爸爸“册手腕”的游戏中,下列说法正确的是( )


| A. | 孩子对爸爸的力与爸爸对孩子的力是两种不同性质的力 | |
| B. | 若爸爸“册倒”孩子,爸爸对孩子的力大于孩子对爸爸的力 | |
| C. | 若孩子“册倒”爸爸,可能是孩子对爸爸施加力的作用先于爸爸又孩子施加力的作用 | |
| D. | 无论谁“册倒”谁,爸爸对孩子的力总等于孩子对爸爸的力 |
2.某校两个课外活动小组分别用以下两种方法来验证机械能守恒定律.请阅读下列两段材料,完成后面问题.

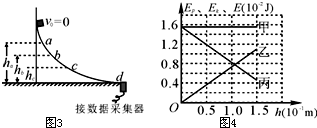
(1)第1小组:利用竖直上抛小球的频闪照片验证机械能守恒定律.如图2所示,图中数据为实际距离,t0时刻刚好对应抛出点,该小组同学通过计算得到不同时刻的速度和速度的平方值如下表,当他们要计算重力势能的改变量时,发现需要先计算当地重力加速度,请你根据实验数据,按照下列要求计算出重力加速度(忽略空气阻力的影响).
①在所给的图1坐标纸上作出v2-h图象;
②分析说明,图象斜率的绝对值表示的物理意义是:重力加速度的二倍;
③由图象求得的重力加速度是9.61m/s2(结果保留三位有效数字).
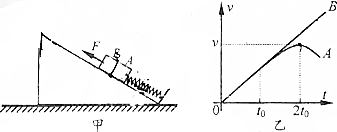
(2)第2小组:DIS实验是利用现代信息技术进行的实验.“用DIS研究机械能守恒定律”的实验装置如图3所示,小组同学在实验中利用小铁块从很光洁的曲面上滑下,选择DIS以图象方式显示实验的结果,所显示的图象如图4所示.图象的横轴表示小铁块距d点(最低点)的高度h,纵轴表示小铁块的重力势能EP、动能Ek或机械能E.试回答下列问题:
①图4的图象中,表示小铁块的重力势能EP、动能Ek、机械能E随小球距d点的高度h变化关系的图线分别是乙、丙、甲(按顺序填写相应图线所对应的文字);
②根据图4所示的实验图象,可以得出的结论是:在误差允许的范围内,小球下落过程机械能守恒.

(1)第1小组:利用竖直上抛小球的频闪照片验证机械能守恒定律.如图2所示,图中数据为实际距离,t0时刻刚好对应抛出点,该小组同学通过计算得到不同时刻的速度和速度的平方值如下表,当他们要计算重力势能的改变量时,发现需要先计算当地重力加速度,请你根据实验数据,按照下列要求计算出重力加速度(忽略空气阻力的影响).
| 时刻 | t1 | t2 | t3 | t4 | t5 |
| 速度v(m/s) | 4.52 | 4.04 | 3.56 | 3.08 | 2.60 |
| v2(m2/s2) | 20.43 | 16.32 | 12.67 | 9.49 | 6.76 |
②分析说明,图象斜率的绝对值表示的物理意义是:重力加速度的二倍;
③由图象求得的重力加速度是9.61m/s2(结果保留三位有效数字).
(2)第2小组:DIS实验是利用现代信息技术进行的实验.“用DIS研究机械能守恒定律”的实验装置如图3所示,小组同学在实验中利用小铁块从很光洁的曲面上滑下,选择DIS以图象方式显示实验的结果,所显示的图象如图4所示.图象的横轴表示小铁块距d点(最低点)的高度h,纵轴表示小铁块的重力势能EP、动能Ek或机械能E.试回答下列问题:
①图4的图象中,表示小铁块的重力势能EP、动能Ek、机械能E随小球距d点的高度h变化关系的图线分别是乙、丙、甲(按顺序填写相应图线所对应的文字);
②根据图4所示的实验图象,可以得出的结论是:在误差允许的范围内,小球下落过程机械能守恒.

7. 如图所示,在粗糙绝缘的水平面上固定一带负电的点电荷P,在M点无初速释放一带有恒定电荷的小物块,小物块在P的电场中运动到N点静止,则从M点运动到N点的过程中,下面说法正确的是( )
如图所示,在粗糙绝缘的水平面上固定一带负电的点电荷P,在M点无初速释放一带有恒定电荷的小物块,小物块在P的电场中运动到N点静止,则从M点运动到N点的过程中,下面说法正确的是( )
 如图所示,在粗糙绝缘的水平面上固定一带负电的点电荷P,在M点无初速释放一带有恒定电荷的小物块,小物块在P的电场中运动到N点静止,则从M点运动到N点的过程中,下面说法正确的是( )
如图所示,在粗糙绝缘的水平面上固定一带负电的点电荷P,在M点无初速释放一带有恒定电荷的小物块,小物块在P的电场中运动到N点静止,则从M点运动到N点的过程中,下面说法正确的是( )| A. | 小物块所带电荷为正电荷 | |
| B. | 小物块共有的电势能逐渐增大 | |
| C. | 小物块的加速度先减小后增大 | |
| D. | 小物块电势能的减少量等于克服摩擦力做的功 |
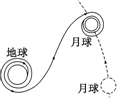 我国已启动了月球探测计划--“嫦娥工程”.如图所示为“嫦娥一号”月球探测器飞行路线的示意图.
我国已启动了月球探测计划--“嫦娥工程”.如图所示为“嫦娥一号”月球探测器飞行路线的示意图. 如图甲所示的装置叫做阿物伍德机,是英国数学家和物理学家阿特伍德(G•Atwood 1746-1807)创新的一种著名力学实验装置,用来研究匀变速直线运动的规律,某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.
如图甲所示的装置叫做阿物伍德机,是英国数学家和物理学家阿特伍德(G•Atwood 1746-1807)创新的一种著名力学实验装置,用来研究匀变速直线运动的规律,某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.