题目内容
6.如图甲所示,平行于光滑斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接、两物块A、B质量均为m,初始时均静止,现用平行于斜面向上的力F拉动物块B,使B做加速度为α的匀加速直线运动,A、B两物块在开始一段时间内的v-t关系分别对应图乙中A、B图线,t0时刻A、B的图线相切,2t0时刻物块A达到最大速度v,重力加速度为g.试求:(1)t0时刻弹簧的压缩量x1;
(2)2t0时刻物块A与物块B之间的距离S;
(3)在t0到2t0时间内,弹簧弹力所做的功W.

分析 (1)由图乙知,在0-t0时间内AB一起匀加速上滑,由位移公式求出位移,由胡克定律求出AB均静止时弹簧的压缩量,从而根据几何关系求出t0时刻弹簧的压缩量x1;
(2)2t0时刻物块A达到最大速度v时,合力为零,由胡克定律和平衡条件求出此时弹簧的压缩量,由位移公式求出B的位移,即可求得2t0时刻物块A与物块B之间的距离S;
(3)在t0到2t0时间内,弹簧弹力所做的功W由动能定理求解.
解答 解:(1)AB均静止时弹簧的压缩量 x0=$\frac{2mgsinθ}{k}$
在0-t0时间内AB一起匀加速上滑,通过的位移为 x=$\frac{1}{2}a{t}_{0}^{2}$
故t0时刻弹簧的压缩量 x1=x0-x=$\frac{2mgsinθ}{k}$-$\frac{1}{2}a{t}_{0}^{2}$.
(2)2t0时刻物块A达到最大速度v时,合力为零,此时弹簧的压缩量为 x2=$\frac{mgsinθ}{k}$
2t0时间内B的位移为 xB=$\frac{1}{2}a(2{t}_{0})^{2}$=2a${t}_{0}^{2}$
故2t0时刻物块A与物块B之间的距离 S=xB-(x0-x2)=2a${t}_{0}^{2}$-$\frac{mgsinθ}{k}$
(3)t0时刻物块AB的速度为 v′=at0.
在t0到2t0时间内,B上滑的位移 xB′=x1-x2=$\frac{mgsinθ}{k}$-$\frac{1}{2}a{t}_{0}^{2}$
对B,由动能定理得:W-mgsinθxB′=$\frac{1}{2}m{v}^{2}-\frac{1}{2}mv{′}^{2}$
可得弹簧弹力所做的功 W=$\frac{{m}^{2}{g}^{2}si{n}^{2}θ}{k}$-$\frac{1}{2}mga{t}_{0}^{2}sinθ$+$\frac{1}{2}m{v}^{2}$-$\frac{1}{2}m{a}^{2}{t}_{0}^{2}$
答:
(1)t0时刻弹簧的压缩量x1是$\frac{2mgsinθ}{k}$-$\frac{1}{2}a{t}_{0}^{2}$.
(2)2t0时刻物块A与物块B之间的距离S是2a${t}_{0}^{2}$-$\frac{mgsinθ}{k}$.
(3)在t0到2t0时间内,弹簧弹力所做的功W是$\frac{{m}^{2}{g}^{2}si{n}^{2}θ}{k}$-$\frac{1}{2}mga{t}_{0}^{2}sinθ$+$\frac{1}{2}m{v}^{2}$-$\frac{1}{2}m{a}^{2}{t}_{0}^{2}$.
点评 解决本题的关键要正确分析物体的位移与弹簧形变量之间的几何关系,知道B速度最大的条件,再运用胡克定律、动力学规律结合研究.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 10年 | B. | 100 年 | C. | 103年 | D. | 104年 |
| A. | $\sqrt{\frac{k}{n}}M$ | B. | $\frac{{n}^{3}}{{k}^{2}}M$ | C. | $\frac{n}{k}M$ | D. | $\frac{{n}^{3}}{{k}^{3}}M$ |
| A. | 由R=$\frac{U}{I}$可知,导体的电阻与导体两端电压成正比,与流过导体的电流成反比 | |
| B. | 由R=$\frac{ρl}{S}$可知,导体的电阻与导体的长度成正比,与导体的横截面积成反比 | |
| C. | 由ρ=$\frac{ρl}{S}$可知,导体的电阻率与导体的横截面积成正比,与导体的长度成反比 | |
| D. | 导体的电阻率只与材料的种类决定,跟温度无关 |
| A. | 1m/s2,方向向北 | B. | 1m/s2,方向向南 | C. | 4m/s2,方向向北 | D. | 4m/s2,方向向南 |

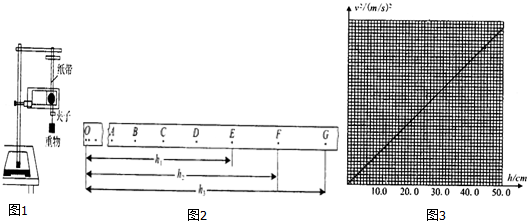
 如图所示,一个透明玻璃球的折射率为$\sqrt{2}$,一束足够强的细光束在过球心的平面内,以45°入射角由真空射入玻璃球后,在玻璃球与真空的交界面处发生多次反射和折射,从各个方向观察玻璃球,能看到从玻璃球内射出的光线的条数是( )
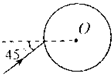
如图所示,一个透明玻璃球的折射率为$\sqrt{2}$,一束足够强的细光束在过球心的平面内,以45°入射角由真空射入玻璃球后,在玻璃球与真空的交界面处发生多次反射和折射,从各个方向观察玻璃球,能看到从玻璃球内射出的光线的条数是( ) 一转动装置如图甲所示,两根足够长轻杆OA、OB固定在竖直轻质转轴上的O点,两轻杆与转轴间夹角均为30°,小球a、b分别套在两杆上,小环c套在转轴上,球与环质量均为m,c与a、b间均用长为L的细线相连,原长为L的轻质弹簧套在转轴上,且与轴上P点、环c相连.当装置以某一转速转动时,弹簧伸长到$\frac{3}{2}L$,环c静止在O处,此时弹簧弹力等于环的重力,球、环间的细线刚好拉直而无张力.弹簧始终在弹性限度内,忽略一切摩擦和空气阻力,重力加速度为g.求:
一转动装置如图甲所示,两根足够长轻杆OA、OB固定在竖直轻质转轴上的O点,两轻杆与转轴间夹角均为30°,小球a、b分别套在两杆上,小环c套在转轴上,球与环质量均为m,c与a、b间均用长为L的细线相连,原长为L的轻质弹簧套在转轴上,且与轴上P点、环c相连.当装置以某一转速转动时,弹簧伸长到$\frac{3}{2}L$,环c静止在O处,此时弹簧弹力等于环的重力,球、环间的细线刚好拉直而无张力.弹簧始终在弹性限度内,忽略一切摩擦和空气阻力,重力加速度为g.求: