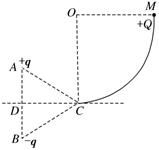
题目内容
如图所示,同一竖直线上的A、B两点,固定有等量的异种点电荷,电荷量为q,正、负如图所示,△ABC为一等边三角形(边长为L),CD为AB边的中垂线,且与右侧竖直光滑![]() 圆弧轨道的最低点C相切,已知圆弧的半径为R,现把质量为m、带电荷量为+Q的小球(可视为质点)由圆弧的最高点M静止释放,到最低点C时速度为v0.已知静电力常量为k,现取D为电势零点,求:
圆弧轨道的最低点C相切,已知圆弧的半径为R,现把质量为m、带电荷量为+Q的小球(可视为质点)由圆弧的最高点M静止释放,到最低点C时速度为v0.已知静电力常量为k,现取D为电势零点,求:
(1)小球在C点受到的电场力的大小和方向;
(2)在等量异种点电荷的电场中,M点的电势φM.
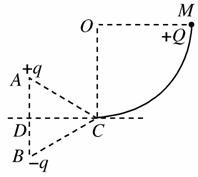
解析:(1)小球到达最低点C时,+q与-q对其的电场力F1、F2是大小相等的,有F1=F2=k![]()
又因为△ABC为等边三角形,易知F1、F2的夹角是120°,所以二者的合力为F12=k![]() ,且方向竖直向下.
,且方向竖直向下.
(2)小球由最高点M运动到C的过程中,由动能定理得
mgR+QUMC=![]() mv
mv![]()
可得M、C两点的电势差为
UMC=![]() (mv
(mv![]() -2mgR)
-2mgR)
又等量异种点电荷中垂线上的电势相等,即C、D两点电势相等,故M点的电势为
φM=UMC=![]() (mv
(mv![]() -2mgR).
-2mgR).
答案: (1)k![]() 方向竖直向下 (2)
方向竖直向下 (2)![]() (mv
(mv![]() -2mgR)
-2mgR)

练习册系列答案
相关题目
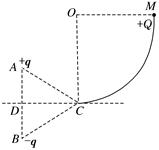
 如图所示,同一竖直线的A、B两点固定有等量异种点电荷,电量为q,正负如图所示,△ABC为一等边三角形(边长为L),CD为AB边的中垂线,且与右侧竖直光滑
如图所示,同一竖直线的A、B两点固定有等量异种点电荷,电量为q,正负如图所示,△ABC为一等边三角形(边长为L),CD为AB边的中垂线,且与右侧竖直光滑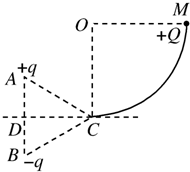 如图所示,同一竖直线上的A、B两点,固定有等量的异种点电荷,电荷量为q,正、负如图所示,△ABC为一等边三角形(边长为L),CD为AB边的中垂线,且与右侧竖直光滑
如图所示,同一竖直线上的A、B两点,固定有等量的异种点电荷,电荷量为q,正、负如图所示,△ABC为一等边三角形(边长为L),CD为AB边的中垂线,且与右侧竖直光滑