题目内容
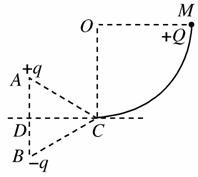
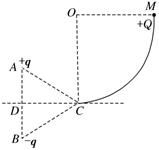
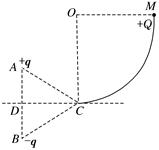
 如图所示,同一竖直线的A、B两点固定有等量异种点电荷,电量为q,正负如图所示,△ABC为一等边三角形(边长为L),CD为AB边的中垂线,且与右侧竖直光滑
如图所示,同一竖直线的A、B两点固定有等量异种点电荷,电量为q,正负如图所示,△ABC为一等边三角形(边长为L),CD为AB边的中垂线,且与右侧竖直光滑| 1 | 4 |
(1)在等量异种电荷A、B的电场中,M点的电势φM
(2)在最低点C轨道对小球的支持力FN多大?
分析:(1)根据动能定理求出QC两点间的电势差,因为等量异种电荷的垂直平分线是等势线,所以C、D的电势相等,则C点的电势等于0,所以M点的电势等于MC的电势差.
(2)小球在C点受重力、支持力、等量异种电荷的库仑力,根据牛顿第二定律求出在最低点C轨道对小球的支持力.
(2)小球在C点受重力、支持力、等量异种电荷的库仑力,根据牛顿第二定律求出在最低点C轨道对小球的支持力.
解答:解:(1)小球由最高点M运动到C的过程中,由动能定理得,
mgR+QUMC=
mv2
可得MC两点的电势差UMC=
又等量异种电荷中垂线上的电势相等,即C、D是等电势的,M点的电势φM=UMC=
.
(2)+Q到达最低点C时,+q与-q对其的电场力F1、F2是大小相等的,有:F1=F2=k
又因为△ABC为等边三角形,知F1、F2的夹角是120°,所以二者的合力为F12=k
,且方向竖直向下的.
由牛顿第二定律得,FN-mg-F12=m
整理得,轨道对小球的支持力FN=mg+m
+k
.
答:(1)在等量异种电荷A、B的电场中,M点的电势为
.
(2)在最低点C轨道对小球的支持力FN=mg+m
+k
.
mgR+QUMC=
| 1 |
| 2 |
可得MC两点的电势差UMC=
| mv2-2mgR |
| 2Q |
又等量异种电荷中垂线上的电势相等,即C、D是等电势的,M点的电势φM=UMC=
| mv2-2mgR |
| 2Q |
(2)+Q到达最低点C时,+q与-q对其的电场力F1、F2是大小相等的,有:F1=F2=k
| L2 |
又因为△ABC为等边三角形,知F1、F2的夹角是120°,所以二者的合力为F12=k
| L2 |
由牛顿第二定律得,FN-mg-F12=m
| v02 |
| R |
整理得,轨道对小球的支持力FN=mg+m
| v02 |
| R |
| L2 |
答:(1)在等量异种电荷A、B的电场中,M点的电势为
| mv2-2mgR |
| 2Q |
(2)在最低点C轨道对小球的支持力FN=mg+m
| v02 |
| R |
| L2 |
点评:本题综合运用了动能定理、牛顿第二定律,关键是正确地进行受力分析,运用合适的规律进行求解.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
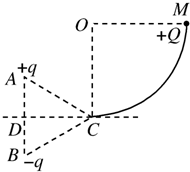 如图所示,同一竖直线上的A、B两点,固定有等量的异种点电荷,电荷量为q,正、负如图所示,△ABC为一等边三角形(边长为L),CD为AB边的中垂线,且与右侧竖直光滑
如图所示,同一竖直线上的A、B两点,固定有等量的异种点电荷,电荷量为q,正、负如图所示,△ABC为一等边三角形(边长为L),CD为AB边的中垂线,且与右侧竖直光滑