��Ŀ����
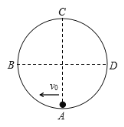
����Ŀ����ͼ��ʾ������ֱ���ڹ̶���һ�뾶ΪR��Բ����AC��Բ����ֱֱ����BD��Բ��ˮƽֱ������Բ��ABC�ǹ⻬�ģ���Բ��CDA�Ǵֲڵġ�һ����ΪmС����Ϊ�ʵ㣩��Բ�����ڲ�A���ô�СΪv0������ˮƽ������ٶȣ�С��պ��ܵڶ��ε���C�㣬�������ٶȴ�СΪg���ڴ˹����У�������
A. С����ʧ�Ļ�е��Ϊ![]()
B. С��ͨ��A��ʱ����ʧ��״̬
C. С���һ�ε���C��ʱ�ٶ�Ϊ![]()
D. С���һ�ε���B��ʱ�ܵ�Բ���ĵ�����СΪ![]()
���𰸡�A
��������
A�����������̿˷�Ħ��������ΪW�����ݶ��ܶ����ã���mg2R��W![]() ���պ��ܵڶ��ε���C�㣬��mg
���պ��ܵڶ��ε���C�㣬��mg![]() �����ݹ��ܹ�ϵ�ã�Q��W����ã�Q
�����ݹ��ܹ�ϵ�ã�Q��W����ã�Q![]() mgR����A��ȷ��
mgR����A��ȷ��
B����A����������֧�����ĺ����ṩ����������FN1��mg��m![]() ����FN1��mg+m
����FN1��mg+m![]() mg����С��ͨ��A��ʱ���ڳ���״̬����B����
mg����С��ͨ��A��ʱ���ڳ���״̬����B����
C��С���һ�ε���C��Ĺ����ɶ��ܶ����ã���mg2R![]() ����ã�vC
����ã�vC![]() ����C����
����C����
D��С���һ�ε���B��Ĺ����ɶ��ܶ����ã���mgR![]() ����B����ţ�ٵڶ����ɵã�N
����B����ţ�ٵڶ����ɵã�N![]() ����ã�N��m��
����ã�N��m��![]() 2g������D����
2g������D����

��ϰ��ϵ�д�
�����Ŀ