题目内容
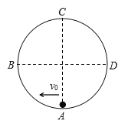
【题目】如图所示，两木块a和b在水平地面上相向运动，它们与地面间的动摩擦因数均为μ＝0.2。在零时刻，两木块相距d＝17 m，木块a的速度大小为va＝10 m/s，木块b的速度大小为vb＝2 m/s；一段时间后，木块a与已停止运动的木块b相碰，碰撞时间极短，碰后两木块粘在一起运动，刚好运动到木块b的零时刻位置停止。重力加速度取g＝10 m/s2。求：
（1）两木块发生碰撞的时刻t；
（2）两木块在碰撞中损失的动能与碰前瞬间总动能的比值。
【答案】（1）2s（2）
【解析】
（1）两物体运动的加速度均为
，
则b从开始运动到停止时的位移：
，
则碰撞时a的位移应该为xa=17m-1m=16m ；
对滑块a：
，即
，
解得t=2s（另一解t=8s舍掉）
（2）碰后两物块一起向右减速到零，其位移为x=xb=1m，加速度仍为a=-2m/s2可知碰后的共同速度
；
碰前a的速度
碰撞过程动量守恒，则：
，
解得
碰前的动能：
碰后动能：
，
则两木块在碰撞中损失的动能与碰前瞬间总动能的比值
练习册系列答案
阅读快车系列答案
相关题目
