题目内容
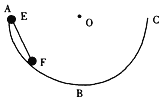
【题目】如图所示,一个竖直放置半径为R的半圆形轨道ABC,B是最低点,AC与圆心O在同一水平高度,![]() 圆弧AB表面是光滑的,圆弧BC表面是粗糙的。现有一根长也为R、质量不计的细杆EF,上端连接质量为m的小球E,下端连接质量为2m的小球F。E球从A点静止释放,两球一起沿轨道下滑,当E球到达最低点B时速度刚好为零。在下滑过程中,F球经过B点的瞬时速度大小是________,在E球从A运动到B的过程中,两球克服摩擦力做功的大小是________。
圆弧AB表面是光滑的,圆弧BC表面是粗糙的。现有一根长也为R、质量不计的细杆EF,上端连接质量为m的小球E,下端连接质量为2m的小球F。E球从A点静止释放,两球一起沿轨道下滑,当E球到达最低点B时速度刚好为零。在下滑过程中,F球经过B点的瞬时速度大小是________,在E球从A运动到B的过程中,两球克服摩擦力做功的大小是________。
【答案】![]() (2﹣
(2﹣![]() )mgR
)mgR
【解析】
E球从A点静止释放到F球经过B点的过程中,系统的机械能守恒,由机械能守恒定律求F球经过B点的瞬时速度大小。对整个过程,根据功能关系求解两球克服摩擦力做功的大小。
[1]设F球经过B点的瞬时速度大小是v,E球从A点静止释放到F球经过B点的过程中,系统的机械能守恒,则得:
![]()
解得:
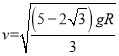 ;
;
[2]设在E球从A运动到B的过程中,两球克服摩擦力做功的大小是W,根据功能关系得知:两球克服摩擦力做功的大小等于系统机械能的减少量,则
![]()
解得:
![]() 。
。

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】用如图所示的实验装置研究平抛运动.某同学按如下的操作得到了一组数据:
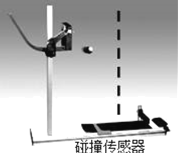
①将碰撞传感器水平放置,在轨道多个位置静止释放小球.
②将碰撞传感器竖直放置在离抛出点一定距离处(图中虚线位置),在轨道多个位置静止释放小球,小球都击中碰撞传感器.
1 | 2 | 3 | 4 | 5 | 6 | |
初速度v0(m/s) | 1.024 | 1.201 | 1.176 | 1.153 | 0.942 | 1.060 |
飞行时间t(s) | 0.246 | 0.249 | 0.248 | 0.173 | 0.212 | 0.189 |
(1)本实验除了碰撞传感器外,还需用到的传感器是__.
(2)根据表格可知,碰撞传感器水平放置时,距离小球抛出点的高度约__m;碰撞传感器竖直放置时,距离小球抛出点的水平距离约__m.