题目内容
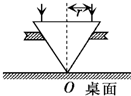在桌面上有一倒立的玻璃圆锥，其顶点恰好与桌面接触，圆锥的轴（图甲中虚线）与桌面垂直，过轴线的截面为等边三角形，如图所示．有一半径为r的圆柱形的平行光束垂直入射到圆锥的底面上，光束的中心轴与圆锥的轴重合．已知玻璃的折射率为1.6，则光束在桌面上形成的光斑面积为（ ）分析：当半径为r的圆柱形平行光束垂直入射到圆锥的地面上，经过第一次折射时，入射角等于零，所以折射角也是零，光线方向不变．当第二次折射时，由于入射角等于60°，而玻璃的折射率为1.6，可得临界角小于45°，所以会发生光的全反射，反射光线却恰好垂直射出．可先根据几何关系可确定光斑的半径，再求解光斑面积．
解答：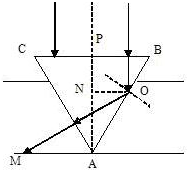
解：设玻璃的临界角为C，则有sinC=
=
＜
，则临界角C＜45°．
经过第一次折射时，由于入射角等于零，所以折射角也是零，因此折射光线不发生偏折．
当第二次折射时，由于入射角等于60°．所以会BA面上发生全反射，几何知识得到反射光线恰好垂直射出．
由题，ON=r，则OA=2r．
由于∠MOA=∠AMO=30°，所以光斑的半径AM=2r．
则光斑的面积S=π（2r）2=4πr2
故选B
解：设玻璃的临界角为C，则有sinC=| 1 |
| n |
| 1 |
| 1.6 |
| 1 | ||
|
经过第一次折射时，由于入射角等于零，所以折射角也是零，因此折射光线不发生偏折．
当第二次折射时，由于入射角等于60°．所以会BA面上发生全反射，几何知识得到反射光线恰好垂直射出．
由题，ON=r，则OA=2r．
由于∠MOA=∠AMO=30°，所以光斑的半径AM=2r．
则光斑的面积S=π（2r）2=4πr2
故选B
点评：本题解题关键在于是借助于光的折射与反射定律作出光路图，同时利用几何关系来辅助计算．
练习册系列答案
相关题目
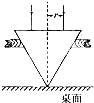（2007?浙江）在桌面上有一倒立的玻璃圆锥，其顶点恰好与桌面接触，圆锥的轴（图中虚线）与桌面垂直，过轴线的截面为等边三角形，如图所示．有一半径为r的圆柱形平行光束垂直入射到圆锥的地面上，光束的中心轴与圆锥的轴重合．已知玻璃的折射率为1.5，则光束在桌面上形成的光斑半径为（ ）
（2009?盐城模拟）（1）A、B、C是三个完全相同的时钟，A放在地面上，B、C分别放在两个高速运动的火箭上，B、C两火箭朝同一方向飞行，速度分别为vB、vC，vB＜vC．地面上观察者认为三个时钟中走得最慢的是
（6分）在桌面上有一倒立的玻璃圆锥，其顶点恰好与桌面接触，圆锥的轴（图中虚线） 与桌面垂直，过轴线的截面为等边三角形，如图所示。有一半径为r的圆柱形平行光束垂直入射到圆锥的地面上，光束的中心轴与圆锥的轴重合。已知玻璃的折射率为1.5，则光束在桌面上形成的光斑半径为多少？