题目内容
（2009?盐城模拟）（1）A、B、C是三个完全相同的时钟，A放在地面上，B、C分别放在两个高速运动的火箭上，B、C两火箭朝同一方向飞行，速度分别为vB、vC，vB＜vC．地面上观察者认为三个时钟中走得最慢的是C
C
；走得最快的是A
A
．（2）如图所示是一列沿x轴向右传播的简谐横波在t=0时刻的波形图，已知波的传播速度v=2m/s．则波的周期为
1s
1s
，图中质点P的振动方向向上
上
（填“上“、“下“、“左“或“右“）．（3）在桌面上有一倒立的玻璃圆锥，其顶点恰好与桌面接触，圆锥的轴（图中虚线）与桌面垂直，过轴线的截面为等边三角形，如图所示．有一半径为r的圆柱形平行光束垂直入射到圆锥的地面上，光束的中心轴与圆锥的轴重合．已知玻璃的折射率为1.5，则光束在桌面上形成的光斑半径为
2r
2r
．分析：（1）根据相对论效应（钟慢效应）分析钟的快慢．
（2）由波形图读出波长，由波速公式v=
求出周期T．根据波形的平移法判断P点的振动方向．
（3）当半径为r的圆柱形平行光束垂直入射到圆锥的地面上，经过第一次折射时，由于入射角等于零，所以折射角也是零，因此折射光线不发生偏折．当第二次折射时，由于入射角等于60°，而玻璃的折射率为1.5，可得临界角小于45°，所以会发生光的全反射，反射光线却恰好垂直射出．故可根据几何关系可确定光斑的半径．
（2）由波形图读出波长，由波速公式v=
| λ |
| T |
（3）当半径为r的圆柱形平行光束垂直入射到圆锥的地面上，经过第一次折射时，由于入射角等于零，所以折射角也是零，因此折射光线不发生偏折．当第二次折射时，由于入射角等于60°，而玻璃的折射率为1.5，可得临界角小于45°，所以会发生光的全反射，反射光线却恰好垂直射出．故可根据几何关系可确定光斑的半径．
解答：解：（1）A放在地面上，在地面上的人看来，A钟快慢没有变化．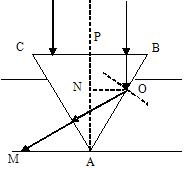
B、C两钟放在两个火箭上，根据爱因斯坦相对论可知，B、C变慢，由于vB＜vC，C钟比B钟更慢，所以C钟最慢，A钟最快．
（2）由波形图知：波长λ=2m，由波速公式v=
得：周期T=
=
s=1s．
简谐横向右传播，波形向右平移，则根据波形的平移法判断得知P点的振动方向向上．
（3）如图所示，
玻璃的折射率为1.5，可得临界角小于45°，经过第一次折射时，由于入射角等于零，所以折射角也是零，因此折射光线不发生偏折．当第二次折射时，由于入射角等于60°．所以会发生光的全反射，反射光线却恰好垂直射出．因为ON等于r，则OA等于2r，由于∠MOA=∠AMO=30°，所以AM等于2r．即光斑半径为2r．
故答案为：
（1）C，A；（2）1s，上；（3）2r
B、C两钟放在两个火箭上，根据爱因斯坦相对论可知，B、C变慢，由于vB＜vC，C钟比B钟更慢，所以C钟最慢，A钟最快．
（2）由波形图知：波长λ=2m，由波速公式v=
| λ |
| T |
| λ |
| v |
| 2 |
| 2 |
简谐横向右传播，波形向右平移，则根据波形的平移法判断得知P点的振动方向向上．
（3）如图所示，
玻璃的折射率为1.5，可得临界角小于45°，经过第一次折射时，由于入射角等于零，所以折射角也是零，因此折射光线不发生偏折．当第二次折射时，由于入射角等于60°．所以会发生光的全反射，反射光线却恰好垂直射出．因为ON等于r，则OA等于2r，由于∠MOA=∠AMO=30°，所以AM等于2r．即光斑半径为2r．
故答案为：
（1）C，A；（2）1s，上；（3）2r
点评：本题要理解记住爱因斯坦相对论效应之一：钟慢效应．要能运用波形平移法判断质点的振动方向．对于几何光学，要借助于光的折射与反射定律作出光路图，同时利用几何关系来辅助计算．
练习册系列答案
阅读快车系列答案
相关题目
（2009?盐城模拟）如图所示，一个质量为m、带电荷量为+q的物体处于场强按E=kt规律（k为大于零的常数，取水平向左为正方向）变化的电场中，物体与绝缘竖直墙壁间的动摩擦因数为μ，当t=0时，物体由静止释放．若最大静摩擦力等于滑动摩擦力，且电场空间和墙面均足够大，下列说法正确的是（ ）
（2009?盐城模拟）如图所示，位于光滑水平面桌面上的小滑块P和Q都视作质点，质量均为m．与轻质弹簧相连．设Q静止，P以某一初速度v向Q运动并与弹簧发生碰撞．在整个过程中，弹簧具有的最大弹性势能等于
（2009?盐城模拟）在如图（a）所示的电路中，R1为定值电阻，R2为滑动变阻器．闭合电键S，将滑动变阻器的滑动触头P从最右端滑到最左端，两个电压表的示数随电路中电流变化的完整过程图线如图（b）所示．则（ ）