题目内容
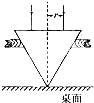（2007?浙江）在桌面上有一倒立的玻璃圆锥，其顶点恰好与桌面接触，圆锥的轴（图中虚线）与桌面垂直，过轴线的截面为等边三角形，如图所示．有一半径为r的圆柱形平行光束垂直入射到圆锥的地面上，光束的中心轴与圆锥的轴重合．已知玻璃的折射率为1.5，则光束在桌面上形成的光斑半径为（ ）分析：当半径为r的圆柱形平行光束垂直入射到圆锥的地面上，经过第一次折射时，由于入射角等于零，所以折射角也是零，因此折射光线不发生偏折．当第二次折射时，由于入射角等于60°，而玻璃的折射率为1.5，可得临界角小于45°，所以会发生光的全反射，反射光线却恰好垂直射出．故可根据几何关系可确定光斑的半径．
解答：解：如图所示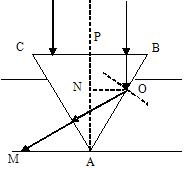
，
玻璃的折射率为1.5，可得临界角小于45°，经过第一次折射时，由于入射角等于零，所以折射角也是零，因此折射光线不发生偏折．当第二次折射时，由于入射角等于60°．所以会发生光的全反射，反射光线却恰好垂直射出．因为ON等于r，则OA等于2r，由于∠MOA=∠AMO=30°，所以AM等于2r．
故选：C
，玻璃的折射率为1.5，可得临界角小于45°，经过第一次折射时，由于入射角等于零，所以折射角也是零，因此折射光线不发生偏折．当第二次折射时，由于入射角等于60°．所以会发生光的全反射，反射光线却恰好垂直射出．因为ON等于r，则OA等于2r，由于∠MOA=∠AMO=30°，所以AM等于2r．
故选：C
点评：本题关键之处是借助于光的折射与反射定律作出光路图，同时利用几何关系来辅助计算．
练习册系列答案
相关题目
（2007?浙江）如图所示，质量为m的由绝缘材料制成的球与质量为M=19m的金属球并排悬挂．现将绝缘球拉至与竖直方向成θ=60°的位置自由释放，下摆后在最低点与金属球发生弹性碰撞．在平衡位置附近存在垂直于纸面的磁场．已知由于磁场的阻尼作用，金属球将于再次碰撞前停在最低点处．求经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于45°．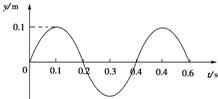
（2007?浙江）一列简谐横波沿x轴负方向传播，波速为v=4m/s．已知坐标原点（x=0）处质点的振动图象如图所示，在下列4幅图中能够正确表示t=0.15s时波形的图是（ ）