题目内容
11. 如图所示,水平粗糙轨道AB与半圆形光滑的竖直轨道BC相连,B点和C点的连线沿竖直方向,圆轨道的半径为R=0.8m.一个小滑块以一定初速度从A点开始沿轨道滑动,已知它运动到C点时对轨道的压力大小恰好等于其重力,g取10m/s2.求:
如图所示,水平粗糙轨道AB与半圆形光滑的竖直轨道BC相连,B点和C点的连线沿竖直方向,圆轨道的半径为R=0.8m.一个小滑块以一定初速度从A点开始沿轨道滑动,已知它运动到C点时对轨道的压力大小恰好等于其重力,g取10m/s2.求:(1)滑块在C点时的速度.
(2)滑块离开C点至着地时的水平射程.
分析 根据牛顿第二定律求出C点的速度大小,根据高度求出平抛运动的时间,结合初速度和时间求出水平射程.
解答 解:(1)在C点,根据牛顿第二定律得,$mg+{F}_{N}=m\frac{{{v}_{C}}^{2}}{R}$,
解得${v}_{C}=\sqrt{2gR}$=$\sqrt{2×10×0.8}m/s=4m/s$.
(2)根据$2R=\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{4R}{g}}=\sqrt{\frac{4×0.8}{10}}s=0.4\sqrt{2}$s,
则水平射程x=${v}_{C}t=4×0.4\sqrt{2}m=1.6\sqrt{2}m$.
答:(1)滑块在C点的速度为4m/s.
(2)滑块离开C点至着地时的水平射程为$1.6\sqrt{2}$m.
点评 本题考查了圆周运动和平抛运动的基本运用,知道圆周运动向心力的来源,以及平抛运动在水平方向和竖直方向上的运动规律是解决本题的关键.

练习册系列答案
相关题目
2. 一列简谐横波沿x轴正方向传播,t时刻波形图如图中的实线所示,此时波刚好传到P点,t+0.6s时刻,这列波刚好传到Q点,波形如图中的虚线所示,a、b、c、P、Q是介质中的质点,则以下说法正确的是( )
一列简谐横波沿x轴正方向传播,t时刻波形图如图中的实线所示,此时波刚好传到P点,t+0.6s时刻,这列波刚好传到Q点,波形如图中的虚线所示,a、b、c、P、Q是介质中的质点,则以下说法正确的是( )
 一列简谐横波沿x轴正方向传播,t时刻波形图如图中的实线所示,此时波刚好传到P点,t+0.6s时刻,这列波刚好传到Q点,波形如图中的虚线所示,a、b、c、P、Q是介质中的质点,则以下说法正确的是( )
一列简谐横波沿x轴正方向传播,t时刻波形图如图中的实线所示,此时波刚好传到P点,t+0.6s时刻,这列波刚好传到Q点,波形如图中的虚线所示,a、b、c、P、Q是介质中的质点,则以下说法正确的是( )| A. | 这列波的波速为16.7 m/s | |
| B. | 这列波的周期为0.8 s | |
| C. | 质点c在这段时间内通过的路程一定等于30 cm | |
| D. | 从t时刻开始计时,质点a第一次到达平衡位置时,恰好是t+$\frac{1}{3}$s这个时刻 | |
| E. | 当t+0.5 s时刻,质点b、P的位移相同 |
6.一个物体以某一初速度从固定的粗糙斜面的底部上滑,物体滑到最高点后又返回到斜面底部,则( )
| A. | 物体从底部滑到最高点的时间与从最高点返回底部的时间相等 | |
| B. | 上滑过程中弹力的冲量为零 | |
| C. | 上滑过程中重力的冲量小于下滑过程中重力的冲量 | |
| D. | 物体返回到斜面底部时重力的瞬时功率等于刚开始上滑时重力的瞬时功率 |
16.一质量为1kg的质点静止于光滑水平面上,从t=0时起,0~2s秒内受到2N的水平外力作用,下列判断正确的是( )
| A. | 0~2s内物体运动的加速度为是2m/s2 | |
| B. | 0~2s内物体通过的位移为4m | |
| C. | 0~2s内外力的平均功率为8W | |
| D. | 0~2内合力做功8J |

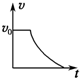
 如图所示,竖直平面内一具有理想边界AB的匀强磁场垂直纸面向里,在距离边界H处一正方形线框MNPO以初速度v0向上运动,假设在整个过程中MN始终与AB平行,则下列图象能反映线框从开始至到达最高点的过程中速度变化规律的是( )
如图所示,竖直平面内一具有理想边界AB的匀强磁场垂直纸面向里,在距离边界H处一正方形线框MNPO以初速度v0向上运动,假设在整个过程中MN始终与AB平行,则下列图象能反映线框从开始至到达最高点的过程中速度变化规律的是( )


 如图所示,电动机通过其转轴上的绝缘细绳牵引一根原来静止的长为L=1m,质量m=0.1kg的导体棒ab,导体棒紧贴在竖直放置、电阻不计的金属框架上,导体棒的电阻R=1Ω,磁感强度B=1T的匀强磁场方向垂直于导体框架所在平面.当导体棒在电动机牵引下上升h=3.8m时,获得稳定速度,此过程中导体棒产生热量Q=2J.电动机工作时,电压表、电流表的读数分别为U=7v和I=1A,电动机的内阻r=1Ω.不计一切摩擦,g取10m/s2.求:
如图所示,电动机通过其转轴上的绝缘细绳牵引一根原来静止的长为L=1m,质量m=0.1kg的导体棒ab,导体棒紧贴在竖直放置、电阻不计的金属框架上,导体棒的电阻R=1Ω,磁感强度B=1T的匀强磁场方向垂直于导体框架所在平面.当导体棒在电动机牵引下上升h=3.8m时,获得稳定速度,此过程中导体棒产生热量Q=2J.电动机工作时,电压表、电流表的读数分别为U=7v和I=1A,电动机的内阻r=1Ω.不计一切摩擦,g取10m/s2.求: 如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将长为L、质量为m的导体棒由静止释放,当导体棒下滑距离L时达最大速度v(v为未知量),导体棒始终与导轨垂直且接触良好,导体棒的电阻为2R,不计导轨的电阻,重力加速度为g,求:
如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将长为L、质量为m的导体棒由静止释放,当导体棒下滑距离L时达最大速度v(v为未知量),导体棒始终与导轨垂直且接触良好,导体棒的电阻为2R,不计导轨的电阻,重力加速度为g,求: