题目内容
如图所示,光滑的
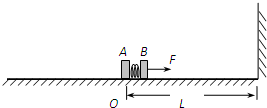
圆弧轨道AB、EF,半径AO、O′F均为9且水平.质量为m、长度也为9的小车静止在光滑水平面CD上,小车上表面与轨道AB、EF的末端B、E相切.一质量为m的物体(可视为质点)从轨道AB的A点由静止开始下滑,由末端B滑上小车,小车立即向4运动.当小车4端与壁DE刚接触时,物体m恰好滑动到小车4端且相对于小车静止,同时小车与壁DE相碰后立即停止运动但不粘连,物体继续运动滑上圆弧轨道EF,以后又滑下来冲上小车.求:
(1)水平面CD的长度;
(2)物体m滑上轨道EF的最高点相对于E点的高度h;
(3)当物体再从轨道EF滑下并滑上小车后,小车立即向左运动.如果小车与壁BC相碰后速度也立即变为零,最后物体m停在小车上的Q点,则Q点距小车4端多远?

| 1 |
| 4 |
(1)水平面CD的长度;
(2)物体m滑上轨道EF的最高点相对于E点的高度h;
(3)当物体再从轨道EF滑下并滑上小车后,小车立即向左运动.如果小车与壁BC相碰后速度也立即变为零,最后物体m停在小车上的Q点,则Q点距小车4端多远?

(l)设物体从A滑至B点时速度为v多,根据机械能守恒,有
mgR=
mv
设小车与壁DE刚接触时物体及小车达到的共同速度为vl,根据动量守恒定律,有
mv多=2mvl
设二者之间摩擦力为f,则
对物体:-fgsCD=
m
-
mv
对小车:f(sCD-R)=
m
解3:sCD=
R
(2)车与ED相碰后,物体以速度vl冲上EF,则
m
=mgh,
解3:h=
(3)由第(l)问可求3:f=
mg,vl=
物体从轨道EF滑下并再次滑上小车后,设它们再次达到共同速度为v2,物体相对车滑行距离sl,则mvl=2mv2
fsl=
m
-
×2m
,
解3:sl=
R
sl<R,说明在车与BC相碰之前,车与物体达到相对静止,以后一起匀速运动直到小车与壁BC相碰.车停止后物体将做匀减速运动,设相对车滑行距离s2,则
fs2=
m
,
解3:s2=
R
所以物体最后距车右端 s总=sl+s2=
R
答:
(l)水平面CD的长度为
R;
(2)物体m滑上轨道EF的最高点相对于E点的高度h为
;
(3)当物体再从轨道EF滑下并滑上小车后,小车立即向左运动.如果小车与壁BC相碰后速度也立即变为零,最后物体m停在小车上的Q点,则Q点距小车右端为
R.
mgR=
| l |
| 2 |
| 2多 |
设小车与壁DE刚接触时物体及小车达到的共同速度为vl,根据动量守恒定律,有
mv多=2mvl
设二者之间摩擦力为f,则
对物体:-fgsCD=
| l |
| 2 |
| v | 2l |
| l |
| 2 |
| 2多 |
对小车:f(sCD-R)=
| l |
| 2 |
| v | 2l |
解3:sCD=
| 3 |
| 2 |
(2)车与ED相碰后,物体以速度vl冲上EF,则
| l |
| 2 |
| v | 2l |
解3:h=
| R |
| 4 |
(3)由第(l)问可求3:f=
| l |
| 2 |
|
物体从轨道EF滑下并再次滑上小车后,设它们再次达到共同速度为v2,物体相对车滑行距离sl,则mvl=2mv2
fsl=
| l |
| 2 |
| v | 2l |
| l |
| 2 |
| v | 22 |
解3:sl=
| l |
| 4 |
sl<R,说明在车与BC相碰之前,车与物体达到相对静止,以后一起匀速运动直到小车与壁BC相碰.车停止后物体将做匀减速运动,设相对车滑行距离s2,则
fs2=
| l |
| 2 |
| v | 22 |
解3:s2=
| l |
| 六 |
所以物体最后距车右端 s总=sl+s2=
| 3 |
| 六 |
答:
(l)水平面CD的长度为
| 3 |
| 2 |
(2)物体m滑上轨道EF的最高点相对于E点的高度h为
| R |
| 4 |
(3)当物体再从轨道EF滑下并滑上小车后,小车立即向左运动.如果小车与壁BC相碰后速度也立即变为零,最后物体m停在小车上的Q点,则Q点距小车右端为
| 3 |
| 六 |

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目