题目内容
6. 如图是交流发电机模型示意图.在磁感应强度为B的匀强磁场中,矩形线圈abcd可绕线圈平面内垂直于磁感线的OO′轴转动,线圈在转动中保持和外电路电阻R形成闭合电路.已知ab长度为L1,bc长度为L2,线圈电阻为r,线圈以恒定角速度ω逆时针转动.(只考虑单匝线圈,不计其他电阻)
如图是交流发电机模型示意图.在磁感应强度为B的匀强磁场中,矩形线圈abcd可绕线圈平面内垂直于磁感线的OO′轴转动,线圈在转动中保持和外电路电阻R形成闭合电路.已知ab长度为L1,bc长度为L2,线圈电阻为r,线圈以恒定角速度ω逆时针转动.(只考虑单匝线圈,不计其他电阻)求:(1)线圈转动过程中产生的最大感应电动势Em;
(2)若线圈经过图示位置时开始计时,写出交变电流的瞬时值表达式;
(3)线圈从图示位置转过90°的过程中电阻R上通过的电荷量.
分析 (1)矩形线圈abcd转动过程中,只有ab和cd切割磁感线,先求出转动线速度,根据Em=BSω求出导线ab和cd因切割磁感线而产生的感应电动势,从而写出瞬时表达式;
(3)求通过的电荷量时,用平均感应电动势;
解答 解:(1)感应电动势的最大值:Em=BSω=BL1L2ω
(2)感应电流的最大值:${I_m}=\frac{E_m}{R+r}=\frac{BSω}{R+r}=\frac{{B{L_1}{L_2}ω}}{R+r}$
所以电流瞬时值表达式:$i={I_m}sinωt=\frac{{B{L_1}{L_2}ω}}{R+r}sinωt$
(3)从图示位置转过90°的过程中:△φ=B△S=BL1L2
$△t=\frac{T}{4}=\frac{π}{2ω}$
平均电动势为:$\overline{E}=\frac{△φ}{△t}$
所以电流为:$\overline{I}=\frac{\bar E}{R+r}=\frac{△φ}{(R+r)△t}$
通过的电荷量为:$q=\bar I△t=\frac{△φ}{(R+r)△t}×△t=\frac{△φ}{R+r}=\frac{{B{L_1}{L_2}}}{R+r}$
答::(1)线圈转动过程中产生的最大感应电动势BL1L2ω;
(2)若线圈经过图示位置时开始计时,写出交变电流的瞬时值表达式$i={I_m}sinωt=\frac{{B{L_1}{L_2}ω}}{R+r}sinωt$;
(3)线圈从图示位置转过90°的过程中电阻R上通过的电荷量$\frac{B{L}_{1}{L}_{2}}{R+r}$
点评 当线圈与磁场相平行时,即线圈边框正好垂直切割磁感线,此时产生的感应电动势最大.求电荷量时,运用交流电的平均值,求产生的热能时,用交流电的有效值

| A. | 电场强度的方向处处与等电势面垂直 | |
| B. | 电场强度为零的地方,电势也为零 | |
| C. | 任一点的电场强度总是指向该点电势降落最快的方向 | |
| D. | 随着电场强度的大小逐渐减小,电势也逐渐降低 |
| A. | 布朗运动是悬浮在液体中固体颗粒的分子无规则运动的反映 | |
| B. | 分子力随分子间的距离的变化而变化,当r>r0时,随着距离的增大,分子间的引力和斥力都增大,但引力比斥力增大的快,故分子力表现为引力 | |
| C. | 两个分子间的距离由很远变到很难再靠近的过程中,分子间作用力的大小将先减小后增大 | |
| D. | 当分子力表现为引力时,分子势能总是随分子间距离的增大而增大 |
 如图所示,竖直光滑杆上套有一个小球和两根弹簧,两弹簧的一端各与小球相连,另一端分别用销钉M、N固定与杆上,小球处于静止状态,设拔去销钉M瞬时,小球加速度的大小为12m/s2,若不拔去销钉M而拔去销钉N瞬间,小球的加速度可能是( )
如图所示,竖直光滑杆上套有一个小球和两根弹簧,两弹簧的一端各与小球相连,另一端分别用销钉M、N固定与杆上,小球处于静止状态,设拔去销钉M瞬时,小球加速度的大小为12m/s2,若不拔去销钉M而拔去销钉N瞬间,小球的加速度可能是( )| A. | 22m/s2,竖直向上 | B. | 22m/s2,竖直向下 | C. | 2m/s2,竖直向上 | D. | 2m/s2,竖直向下 |
 初速度为v0的电子,沿平行于通电长直导线的方向射出,直导线中电流方向与电子的初始运动方向如图所示,则( )
初速度为v0的电子,沿平行于通电长直导线的方向射出,直导线中电流方向与电子的初始运动方向如图所示,则( )| A. | 电子将向左偏转,速率改变 | B. | 电子将向右偏转,速率不变 | ||
| C. | 电子将向左偏转,速率不变 | D. | 电子将向右偏转,速率改变 |
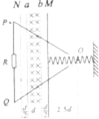 如图所示,阻值为R的电阻串接于光滑的固定在水平面上的等边三角形水平导轨OPQ中,三角形的顶点O处开口,磁感应强度为B、方向竖直向下、宽度为d的条形磁场区域与PQ平行,质量为m的导体棒中点接在劲度系数为k的弹簧的一端,弹簧的另一端固定.导体棒始终与PQ平行,且与导轨保持良好接触,弹簧为自然长度时导体棒静止在M处,现将导体棒拉至N处后自由释放,若M至顶点O距离为2.5d,以及M、N到磁场边沿的距离均为$\frac{d}{2}$,导轨和导体棒的阻值忽略不计,已知弹簧弹性势能Ep与弹簧进度系数k,弹簧形变量x的关系式为Ep=$\frac{1}{2}$kx2,现测得导体棒从N处无初速度释放后第一次向右通过磁场右边界b时的速度为v,求:
如图所示,阻值为R的电阻串接于光滑的固定在水平面上的等边三角形水平导轨OPQ中,三角形的顶点O处开口,磁感应强度为B、方向竖直向下、宽度为d的条形磁场区域与PQ平行,质量为m的导体棒中点接在劲度系数为k的弹簧的一端,弹簧的另一端固定.导体棒始终与PQ平行,且与导轨保持良好接触,弹簧为自然长度时导体棒静止在M处,现将导体棒拉至N处后自由释放,若M至顶点O距离为2.5d,以及M、N到磁场边沿的距离均为$\frac{d}{2}$,导轨和导体棒的阻值忽略不计,已知弹簧弹性势能Ep与弹簧进度系数k,弹簧形变量x的关系式为Ep=$\frac{1}{2}$kx2,现测得导体棒从N处无初速度释放后第一次向右通过磁场右边界b时的速度为v,求:
 在如图所示的匀强电场中,有A、B两点,且A、B两点间的距离为0.20m.已知AB连线与电场线夹角为θ=60°,现把一电荷量为q=2×10-8C带正电的检验电荷放入该匀强电场中,其受到的电场力的大小为F=4.0×10-4N,方向水平向右.求:
在如图所示的匀强电场中,有A、B两点,且A、B两点间的距离为0.20m.已知AB连线与电场线夹角为θ=60°,现把一电荷量为q=2×10-8C带正电的检验电荷放入该匀强电场中,其受到的电场力的大小为F=4.0×10-4N,方向水平向右.求: