题目内容
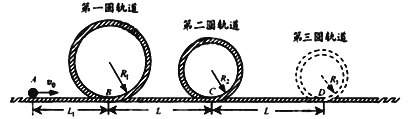
【题目】过山车是游乐场中常见的设施。下图是一种过山车的简易模型，它由水平轨道和在竖直平面内的三个圆形轨道组成，B、C、D分别是三个圆形轨道的最低点，半径
、
。一个质量为
kg的小球（视为质点），从轨道的左侧A点以
的初速度沿轨道向右运动，A、B间距
。小球与水平轨道间的动摩擦因数
，圆形轨道是光滑的。假设水平轨道足够长，圆形轨道间不相互重叠。重力加速度取
，计算结果保留小数点后一位数字。试求：
(1)小球在经过第一个圆形轨道的最高点时，轨道对小球作用力的大小；
(2)如果小球恰能通过第二个圆形轨道，B、C间距L应是多少。
【答案】(1)10.0N；(2)12.5m
【解析】
(1)设小球经过第一个圆轨道的最高点时的速度为v1，根据动能定理得
-μmgL1-2mgR1=
mv12-mv02
小球在最高点受到重力mg和轨道对它的作用力F，根据牛顿第二定律有
F+mg=m
代入数据解得轨道对小球作用力的大小
F=10.0 N
(2)设小球在第二个圆轨道的最高点的速度为v2，小球恰能通过第二圆形轨道，根据牛顿第二定律有
mg=m
根据动能定理
-μmg（L1+L）-2mgR2=mv22-mv02
代入数据解得B、C间距
L=12.5m
练习册系列答案
阅读快车系列答案
相关题目
