题目内容
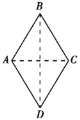
【题目】如图所示,竖直平面内的两个半圆轨道在B点平滑相接,两个半圆的圆心O1、O2在同一水平线上,粗糙的小半圆半径为R,光滑的大半圆的半径为2R;一质量为m的滑块(可视为质点)从大的半圆一端A点以一定的初速度向上沿着半圆内壁运动,且刚好能通过大半圆的最高点,最后滑块从小半圆的左端冲出轨道,刚好能到达大半圆的最高点,已知重力加速度为g,则( )

A.滑块在A点的初速度为![]()
B.滑块在A点对半圆轨道的压力为6mg
C.滑块第一次通过小半圆过程克服摩擦力做的功为mgR
D.增大滑块在A点的初速度,则滑块通过小半圆克服摩擦力做的功不变
【答案】AC
【解析】
A.由于滑块恰好能通过大的半圆的最高点,重力提供向心力,即
mg=m![]() ,
,
解得:
v=![]() ,
,
以AB面为参考面,根据机械能守恒定律可得:
![]() =2mgR+
=2mgR+![]() m(
m(![]() )2,
)2,
求得
vA=![]() ,
,
故A正确;
B.滑块在A点受到圆轨道的支持力为:
F=m![]() =3mg,
=3mg,
由牛顿第三定律可知,滑块在A点对半圆轨道的压力为3mg,故B错误;
C.设滑块在O1点的速度为v1,则:
v1=![]() =2
=2![]() ,
,
在小半圆中运动的过程中,根据动能定理得
Wf=![]() =mgR,
=mgR,
故C正确;
D.增大滑块在A点的初速度,则滑块在小的半圆中各个位置速度都增大,滑块对小半圆轨道的平均压力增大,因此克服摩擦力做的功增多,故D错误。
故选:AC

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目