Question

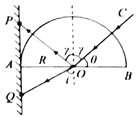
【题目】为判断光信号光纤中的传播时间，工人师傅从抽制光纤内芯的边角料中找到一个端头，并将它打磨成半径为R的半球面，放在竖直屏PQ旁边，让材料的圆面与屏接触，如图所示。现用一束可以转动的光OC射向O点，结果屏上有两个光斑，送渐减小θ时两光斑间距发生变化，当时屏上只有一个光斑。已知光在真空中的传播速度为c,若取用该材料制成长为L的光纤，求：

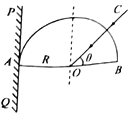
（1）逐渐减小θ时接收屏上的两光斑间距怎样变，并确定是哪侧的光斑先消失；

（2）光信号在光纤中化播的最长时间。

Answer 1

【答案】（1）减小；Q（2）

【解析】(i)（1）光线CO射向O点后，一方面发生折射在屏上出现光斑Q,另一方面发生反射在屏上出现光斑P，逐渐减小θ时，图中的角逐渐增大；

由折射定律知i角也增大；

由几何关系知，因材料的折射率大于1，故；

因此在减小θ时，逐渐增大，PQ减小，即两光斑间距减小；

当角增大到大于等于临界角时折射光线消失，此时屏上只有光斑P；

(ⅱ)由只有一个光斑知临界角为45°，故折射率为；

光纤在传递信息时，光以一定的夹角射入端面后，在光纤侧壁恰好发生全反射的传播时间最长，且光在介质中的速度为；

由全反射知识得，由几何关系知，整理得。