题目内容
宇宙间存在一些离其它恒星较远的、由质量相等的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用.已观测到的四星系统存在着一种基本的构成形式是:三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行,第四颗星位于圆形轨道的圆心处,已知圆形轨道的半径为R,每颗星体的质量均为m.求:
(1)中心星体受到其余三颗星体的引力的大小;
(2)三颗星体沿圆形轨道运动的线速度和周期.
(1)中心星体受到其余三颗星体的引力的大小;
(2)三颗星体沿圆形轨道运动的线速度和周期.
分析: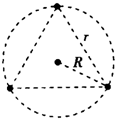 (1)作出中心天体与其余三颗星体的位置关系,由图可知,中心星体受到其余三颗星体的引力大小相等,方向互成1200.
(1)作出中心天体与其余三颗星体的位置关系,由图可知,中心星体受到其余三颗星体的引力大小相等,方向互成1200.
据力的合成法则,中心星体受到其他三颗星体的引力的合力为零.
(2)对圆形轨道上任意一颗星,根据万有引力定律和牛顿第二定律有:
G
+2G
?cos300=m
由几何关系可知,r=2R?cos30°
由次可解得三颗星体运动的线速度v.
则可解得三颗星运动的周期T=
.
 (1)作出中心天体与其余三颗星体的位置关系,由图可知,中心星体受到其余三颗星体的引力大小相等,方向互成1200.
(1)作出中心天体与其余三颗星体的位置关系,由图可知,中心星体受到其余三颗星体的引力大小相等,方向互成1200.据力的合成法则,中心星体受到其他三颗星体的引力的合力为零.
(2)对圆形轨道上任意一颗星,根据万有引力定律和牛顿第二定律有:
G
| m?m |
| R2 |
| m?m |
| r2 |
| v2 |
| R |
由几何关系可知,r=2R?cos30°
由次可解得三颗星体运动的线速度v.
则可解得三颗星运动的周期T=
| 2πR |
| v |
解答: 解:(1)中心星体受到其余三颗星体的引力大小相等,方向互成1200.
解:(1)中心星体受到其余三颗星体的引力大小相等,方向互成1200.
据力的合成法则,中心星体受到其他三颗星体的引力的合力为零.
(2)对圆形轨道上任意一颗星,根据万有引力定律和牛顿第二定律有:
G
+2G
?cos300=m
又因为r=2R?cos30°
由以上两式可得三颗星体运动的线速度为:v=
三颗星运动的周期为:T=
=2πR
答:(1)中心星体受到其余三颗星体的引力的大小为零;
(2)三颗星体沿圆形轨道运动的线速度为
,周期为2πR
.
 解:(1)中心星体受到其余三颗星体的引力大小相等,方向互成1200.
解:(1)中心星体受到其余三颗星体的引力大小相等,方向互成1200.据力的合成法则,中心星体受到其他三颗星体的引力的合力为零.
(2)对圆形轨道上任意一颗星,根据万有引力定律和牛顿第二定律有:
G
| m?m |
| R2 |
| m?m |
| r2 |
| v2 |
| R |
又因为r=2R?cos30°
由以上两式可得三颗星体运动的线速度为:v=
|
三颗星运动的周期为:T=
| 2πR |
| v |
|
答:(1)中心星体受到其余三颗星体的引力的大小为零;
(2)三颗星体沿圆形轨道运动的线速度为
|
|
点评:本题关键势能正确的画出中心星体与其余三颗星体的空间位置关系,根据几何关系确定向心力的来源.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
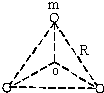 宇宙间存在一些离其它恒星较远的三星系统.其中有一种三星系统如图所示,三颗质量相等的星位于等边三角形的三个顶点上,任意两颗星的距离均为R,并绕其中心O做匀速圆周运动.如果忽略其它星体对它们的引力作用,引力常数为G.以下对该三星系统的说法中正确的是( )
宇宙间存在一些离其它恒星较远的三星系统.其中有一种三星系统如图所示,三颗质量相等的星位于等边三角形的三个顶点上,任意两颗星的距离均为R,并绕其中心O做匀速圆周运动.如果忽略其它星体对它们的引力作用,引力常数为G.以下对该三星系统的说法中正确的是( )| A、每颗星做圆周运动的半径为等边三角形的边长R | B、每颗星做圆周运动的加速度与三星的质量无关 | C、利用所给物理量不能求出每颗星做圆周运动的线速度大小 | D、利用所给物理量能求出每颗星做圆周运动的周期 |
 (2009?奉贤区一模)宇宙间存在一些离其它恒星较远的三星系统.其中有一种三星系统如图所示,三颗质量均为m的星位于等边三角形的三个顶点上,若已知两颗星的距离均为R,如果忽略其它星体对它们的引力作用,三星在同一平面内绕其中心O做匀速圆周运动,周期为T.则每颗星做圆周运动的线速度为
(2009?奉贤区一模)宇宙间存在一些离其它恒星较远的三星系统.其中有一种三星系统如图所示,三颗质量均为m的星位于等边三角形的三个顶点上,若已知两颗星的距离均为R,如果忽略其它星体对它们的引力作用,三星在同一平面内绕其中心O做匀速圆周运动,周期为T.则每颗星做圆周运动的线速度为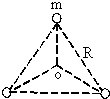 宇宙间存在一些离其它恒星较远的三星系统.其中有一种三星系统如图所示,三颗质量相等的星位于等边三角形的三个顶点上,任意两颗星的距离均为R,并绕其中心O做匀速圆周运动.如果忽略其它星体对它们的引力作用,引力常数为G.以下对该三星系统的说法中正确的是( )
宇宙间存在一些离其它恒星较远的三星系统.其中有一种三星系统如图所示,三颗质量相等的星位于等边三角形的三个顶点上,任意两颗星的距离均为R,并绕其中心O做匀速圆周运动.如果忽略其它星体对它们的引力作用,引力常数为G.以下对该三星系统的说法中正确的是( )

