题目内容
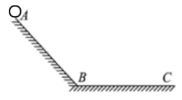
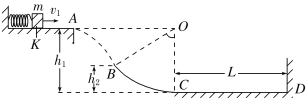
【题目】如图所示,在高h1=30 m的光滑水平平台上,质量m=1 kg的小物块压缩弹簧后被锁扣K锁住,储存了一定量的弹性势能Ep。若打开锁扣K, 小物块将以一定的水平速度v1向右滑下平台,做平抛运动,并恰好能沿光滑圆弧形轨道BC的B点的切线方向进入圆弧形轨道。B点的高度h2=15 m,圆弧轨道的圆心O与平台等高,轨道最低点C的切线水平,并与地面上长为L=50 m的水平粗糙轨道CD平滑连接,小物块沿轨道BCD运动并与右边墙壁发生碰撞,取g=10 m/s2:
(1)求小物块由A到B的运动时间t;
(2)求小物块原来压缩弹簧时储存的弹性势能Ep的大小;
(3)若小物块与墙壁只发生一次碰撞,碰后速度等大反向,反向运动过程中没有冲出B点,最后停在轨道CD上的某点P(P点未画出)。设小物块与轨道CD之间的动摩擦因数为μ,求μ的取值范围。
【答案】(1)![]() s ;(2)50J;(3)
s ;(2)50J;(3)![]() ≤μ<
≤μ<![]()
【解析】
(1)设从A运动到B的时间为t,由平抛运动规律得
h1-h2=![]() gt2
gt2
解得
t=![]() s
s
(2)由![]() ,
,![]() ,所以∠BOC=60°,设物块平抛到B点的水平初速度为v1,将B点速度分解可得
,所以∠BOC=60°,设物块平抛到B点的水平初速度为v1,将B点速度分解可得
![]()
解得
v1=10m/s
根据能量守恒,弹簧的弹性势能转化给物块的动能。得
![]()
(3)设小物块在水平轨道CD上通过的总路程为s,根据题意,该路程的最大值是
smax=3L
路程的最小值是
smin=L
路程最大时,动摩擦因数最小,路程最小时,动摩擦因数最大,由能量守恒知
![]()
![]()
解得
![]() ,
,![]()
由小物块与墙壁只发生一次碰撞可知
![]()

练习册系列答案
相关题目