Question

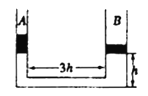
【题目】一物体做加速直线运动，依次经过A、B、C三位置，B为AC的中点，物体在AB段的加速度为a1，在BC段的加速度为a2。现测得B点的瞬时速度vB=（vA+vC），则a1与a2的大小关系为( )

A. a1 >a2B. a1=a2C. a1<a2D. 无法比较

Answer 1

【答案】C

【解析】

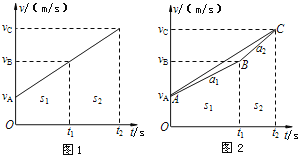
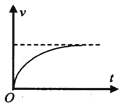
如果物体从A至C的过程中是作匀加速直线运动，则物体的速度图线如图1所示，

因为B点是AC的中点，很显然可以看出图线下所对应的面积S1≠S2，要满足S1=S2的条件，时间t1必须要向右移至图2所示的位置，又因为vB=（vA+vC），这是从A至B匀加速运动过程中的中间时刻的瞬时速度，即t1=t2/2时刻的瞬时速度，但t1时刻所对应的位置又不是AC的中点，要同时满足S1=S2和vB=（vA+vC）的条件，将图1中的时刻t1沿t轴向右移至满足S1=S2位置处，如图2所示，再过vB=（vA+vC）点作平行于时间轴t的平行线交于B点，连接AB得到以加速度a1运动的图线，连接BC得到以加速度a2运动的图线，比较连线AB和BC的斜率大小，不难看出a2>a1，故C正确，ABD错误。

故选：C。