题目内容
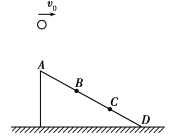
【题目】如图所示,从 A点以v0的水平速度抛出一质量m=2kg的小物块(可视为质点),当小物块运动至B点时,恰好沿切线方向进入固定的光滑圆弧轨道BC,圆弧轨道BC的圆心角α=37°,C点在O点的正下方,圆弧轨道C端切线水平与水平面平滑连接.C点右侧水平面粗糙,在水平面上固定一个弹簧,弹簧的左端D距C点的水平距离为L=0.4m,小物块离开C点后继续在水平面上向弹簧滑去,将弹簧压缩了x=0.1m后停止滑行。小物块和水平面间的动摩擦因数μ=0.2,A、B两点距C点的高度分别为H=0.6 m、h=0.15 m,圆弧半径R=0.75m, cos37°=0.8,sin37°=0.6,g=10 m/s2.求:
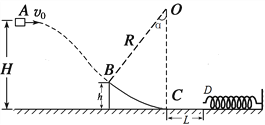
(1)小物块水平抛出时,初速度v0的大小;
(2)小物块滑动至C点时,对圆弧轨道C点的压力大小;
(3) 小物块停止滑行时弹簧具有的弹性势能大小。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)设小物块做平抛运动的时间为t,则有:H-h=![]() gt2
gt2
设小物块到达B点时竖直分速度为vy,有:vy=gt,
由以上两式代入数据解得:vy=3m/s
由题意,速度方向与水平面的夹角为37°,有:tan37°=![]() ,
,
解得:v0=4m/s
(2)设小物块到达C点时速度为v2,从A至C点,由动能定理得:![]()
解得![]()
设C点受到的支持力为FN,则有:FN-mg=![]()
解得FN=![]() N
N
(3)当弹簧压缩到最短时,由能量关系:![]()
解得EP=26J

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目