题目内容
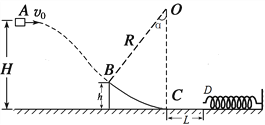
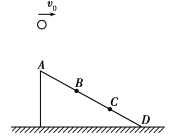
【题目】模拟飞机投弹游戏，从飞机上水平抛出物块击中斜面上的某一个点，如图所示，已知AB=BC=CD。方式一：若飞机悬停在A点的正上方某一不变的位置以不同的初速度
、
抛出两个物块，分别击中斜面上的B点与C点。方式二：若飞机匀速运动，每隔相同的时间放下一个物体，前两个物块分别落在了B、C点，则（）
A. 方式一， 
B. 方式二，第三个物块恰好落在D点
C. 方式二，第三个物块落在水平面上
D. 方式二，第三个物块落在C、D之间
【答案】D
【解析】设抛出点到A点的高度为H，AB、BC、CD之间的水平距离为x，竖直高度差为h；方式一中，落到B点的物体在水平方向的位移：x=v1t1，竖直方向的位移： 
，落在C点的物体在水平方向的位移：2x=v2t2， 竖直方向的位移： 
，联立可得： 
，所以： 
，故A错误；同理，在方式二中，落在B、C、D各点的时间也是不相等的，由位置关系可知：tB＜tC＜tD，由于飞机匀速运动，设速度为v，每隔相同的时间△t放下一个物体，设从落在B点的物体释放时刻开始计时，则落在B点的物体在水平方向的位移：xB=vtB，落在C点的物体的水平位移：xC=v（△t+tC）由题可得则：v（△t+tC）-vtB=x=v△t+v（tC-tB），设第三个物体运动的时间等于落在D点的时间，则：x3=v（2△t+tD），设抛出点到A点的高度为H，AB、BC、CD之间的水平距离为x，竖直高度差为h，则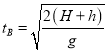
， 
， 
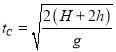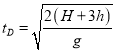。可知：tC-tB＞tD-tC，所以：x3-xB=v（2△t+tD）-vtB=2v△t+（tD-tB）=2v△t+[（tD-tC）+（tC-tB）]＜2v△t+2（tC-tB）=2x，可知即使使用落地D点的时间计算，第三个物体也不能到达D点。则第三个物块一定落在C、D之间，故D正确，BC错误。所以D正确，ABC错误。
