题目内容
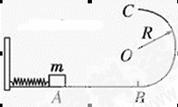
(18分)光滑圆轨道和两倾斜直轨道组成如图所示装置,其中直轨道bc粗糙,直轨道cd光滑,两轨道相接处为一很小的圆弧。质量为m=0.1kg的滑块(可视为质点)在圆轨道上做圆周运动,到达轨道最高点a时的速度大小为v=4m/s,当滑块运动到圆轨道与直轨道bc的相切处b时,脱离圆轨道开始沿倾斜直轨道bc滑行,到达轨道cd上的d点时速度为零。若滑块变换轨道瞬间的能量损失可忽略不计,已知圆轨道的半径为R=0.25m,直轨道bc的倾角 =37o,其长度为L=26.25m,d点与水平地面间的高度差为h=0.2m,取重力加速度g=10m/s2,sin37°=0.6。求:
=37o,其长度为L=26.25m,d点与水平地面间的高度差为h=0.2m,取重力加速度g=10m/s2,sin37°=0.6。求:
(1)滑块在圆轨道最高点a时对轨道的压力大小;
(2)滑块与直轨道bc问的动摩擦因数;
(3)滑块在直轨道bc上能够运动的时间。
(1)5.4N;(2)0.8;(3)7.66s
解析试题分析:(1)在圆轨道最高点a处对滑块由牛顿第二定律得: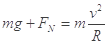
∴ =5.4N
=5.4N
由牛顿第三定律得滑块在圆轨道最高点a时对轨道的压力大小为5.4N
(2) 从a点到d点全程由动能定理得: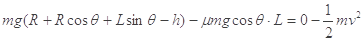
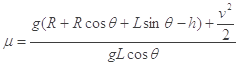 =0.8
=0.8
(3)设滑块在bc上向下滑动的加速度为a1,时间为t1,向上滑动的加速度为a2,时间为t2;在c点时的速度为vc。
由c到d: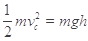
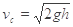 =2m/s
=2m/s
a点到b点的过程: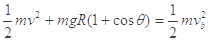
∴ =5m/s
=5m/s
在轨道bc上:
下滑: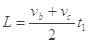
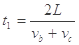 =7.5s
=7.5s
上滑: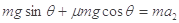
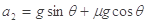 =12.4m/s2
=12.4m/s2 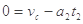
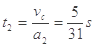 =0.16s
=0.16s
∵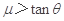 ,∴滑块在轨道bc上停止后不再下滑
,∴滑块在轨道bc上停止后不再下滑
滑块在两个斜面上运动的总时间: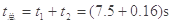 ="7.66s"
="7.66s"
考点:牛顿第二定律及动能定理。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
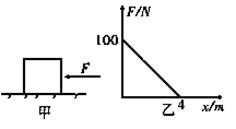
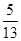 倍。已知杆向上运动时,刚穿过PQ时的速度是刚穿过MN时速度的一半,杆从PQ上升的最大高度(未超过轨道上端)是磁场高度的n倍;杆向下运动时,一进入磁场立即做匀速直线运动。除定值电阻外不计其它一切电阻,已知重力加速度为g。求:
倍。已知杆向上运动时,刚穿过PQ时的速度是刚穿过MN时速度的一半,杆从PQ上升的最大高度(未超过轨道上端)是磁场高度的n倍;杆向下运动时,一进入磁场立即做匀速直线运动。除定值电阻外不计其它一切电阻,已知重力加速度为g。求: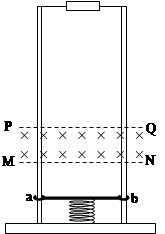
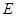 的匀强电场(上、下及左侧无界)。一个质量为
的匀强电场(上、下及左侧无界)。一个质量为 、电量为
、电量为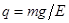 的可视为质点的带正电小球,在
的可视为质点的带正电小球,在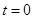 时刻以大小为
时刻以大小为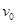 的水平初速度向右通过电场中的一点P,当
的水平初速度向右通过电场中的一点P,当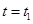 时刻在电场所在空间中加上一如图所示随时间周期性变化的磁场,使得小球能竖直向下通过D点,D为电场中小球初速度方向上的一点,PD间距为
时刻在电场所在空间中加上一如图所示随时间周期性变化的磁场,使得小球能竖直向下通过D点,D为电场中小球初速度方向上的一点,PD间距为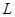 ,D到竖直面MN的距离DQ为
,D到竖直面MN的距离DQ为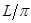 .设磁感应强度垂直纸面向里为正.
.设磁感应强度垂直纸面向里为正.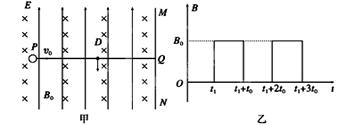
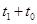 时间内的运动情况,并在图中画出运动的轨迹;
时间内的运动情况,并在图中画出运动的轨迹;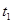 的表达式(用题中所给物理量
的表达式(用题中所给物理量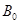 、
、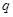 、
、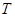 的表达式(用题中所给物理量
的表达式(用题中所给物理量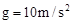 ,结果保留2位有效数字)。
,结果保留2位有效数字)。
