题目内容

某运动员做跳伞训练，他从悬停在空中的直升飞机上由静止跳下，跳离飞机一段时间后打开降落伞做减速下落。他打开降落伞后的速度图线如图a。降落伞用8根对称的绳悬挂运动员，每根绳与中轴线的夹角均为37°，如图b。已知人的质量为50kg，降落伞质量也为50kg，不计人所受的阻力，打开伞后伞所受阻力f与速度v成正比，即f="kv" (g取10m/s2，sin53°=0.8，cos53°="0.6)" ．求：

（1）打开降落伞前人下落的距离为多大？
（2）求阻力系数k和打开伞瞬间的加速度a的大小和方向？
（3）悬绳能够承受的拉力至少为多少？

（1）20m；（2）30m/s2，方向竖直向上；（3）悬绳能承受的拉力为至少为312.5N

解析试题分析:（1）打开降落伞前人做自由落体运动，根据位移速度公式得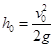：=20m；
（2）由a图可知，当速度等于5m/s时，物体做匀速运动，受力平衡，
则kv=2mg，解得k=200Ns/m
对整体，根据牛顿第二定律得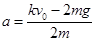：，得，a=30m/s2 
方向竖直向上（1分）
（3）设每根绳的拉力为T，以运动员为研究对象，根据牛顿第二定律得：
8Tcosα-mg=ma，解得T=312.5N
由牛顿第三定律得：悬绳能承受的拉力为至少为312.5N （1分）
考点： 牛顿第二定律；牛顿第三定律

练习册系列答案
相关题目

如图所示，半径为R的光滑圆形轨道在B点与水平轨道AB相切，水平轨道AB在A点与光滑弧形轨道CA相切，轨道CA、AB与圆形轨道都在同一竖直平面内．现让一质量为m的滑块（可视为质点）从弧形轨道上高为h处由静止释放．设滑块与AB轨道的动摩擦因数为μ，AB轨道的长度为x0．为使滑块在进入圆形轨道后能够不脱离轨道而运动，滑块释放的高度h应满足什么条件?（假设B处的缺口不影响滑块进入圆轨道和在圆轨道的上运动）

（18分）光滑圆轨道和两倾斜直轨道组成如图所示装置，其中直轨道bc粗糙，直轨道cd光滑，两轨道相接处为一很小的圆弧。质量为m=0．1kg的滑块（可视为质点）在圆轨道上做圆周运动，到达轨道最高点a时的速度大小为v=4m/s，当滑块运动到圆轨道与直轨道bc的相切处b时，脱离圆轨道开始沿倾斜直轨道bc滑行，到达轨道cd上的d点时速度为零。若滑块变换轨道瞬间的能量损失可忽略不计，已知圆轨道的半径为R=0．25m，直轨道bc的倾角=37o，其长度为L=26．25m，d点与水平地面间的高度差为h=0．2m，取重力加速度g=10m/s2，sin37°=0．6。求：

（1）滑块在圆轨道最高点a时对轨道的压力大小；
（2）滑块与直轨道bc问的动摩擦因数；
（3）滑块在直轨道bc上能够运动的时间。

如图，在竖直平面内有一固定光滑轨道，其中AB是长为R的水平直轨道，BCD是圆心为O、半径为R的圆弧轨道，两轨道相切于B点．在外力作用下，一小球从A点由静止开始做匀加速直线运动，到达B点时撤除外力．已知小球刚好能沿圆轨道经过最高点C，重力加速度大小为g.求：

(1)小球在AB段运动的加速度的大小；
(2)小球从D点运动到A点所用的时间．

（16分）水上滑梯可简化成如图所示的模型，斜槽AB和水平槽BC平滑连接，斜槽AB的竖直高度H=5.0m，倾角θ=37°。BC面与水面的距离h=0.80m，人与AB、BC间的摩擦均忽略不计。取重力加速度g=10m/s2，cos37°=0.8，sin37°=0.6。一同学从滑梯顶端A点无初速地自由滑下，求：

（1）该同学沿斜槽AB下滑时加速度的大小a；
（2）该同学滑到B点时速度的大小vB；
（3）从C点滑出至落到水面的过程中，该同学在水平方向位移的大小x。

有一个冰上木箱的游戏节目，规则是：选手们从起点开始用力推箱一段时间后，放手让箱向前滑动，若箱最后停在桌上有效区域内，视为成功；若箱最后未停在桌上有效区域内就视为失败．其简化模型如图所示，AC是长度为L1＝7 m的水平冰面，选手们可将木箱放在A点，从A点开始用一恒定不变的水平推力推箱，BC为有效区域．已知BC长度L2＝1 m，木箱的质量m＝50 kg，木箱与冰面间的动摩擦因数μ＝0.1.某选手作用在木箱上的水平推力F＝200 N，木箱沿AC做直线运动，若木箱可视为质点，g取10 m/s2.那么该选手要想游戏获得成功，试求：

(1)推力作用在木箱上时的加速度大小；
(2)推力作用在木箱上的时间满足什么条件？

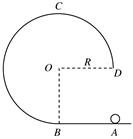
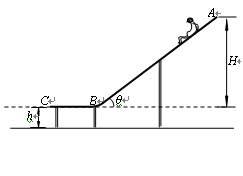
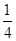如图所示，ABCDO是处于竖直平面内的光滑轨道，AB是半径为R=15m的圆周轨道，半径OA处于水平位置，CDO是直径为15m的半圆轨道，两个轨道如图连接固定。一个小球P从A点的正上方距水平半径OA高H处自由落下，沿竖直平面内的轨道运动。通过CDO轨道的最低点C时对轨道的压力力等于其重力的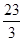倍.取g为10m/s2.

（1）H的大小；
（2）小球沿轨道运动后再次落到轨道上的速度的大小是多少.

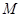如图所示,在质量为的电动机上，装有质量为的偏心轮，偏心轮的重心距转轴的距离为.当偏心轮重心在转轴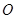正上方时，电动机对地面的压力刚好为零.求电动机转动的角速度.

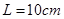（14分）如图所示的电路中，两平行金属板A、B水平放置，极板长，两板间的距离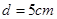.电源的电动势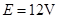，内阻未知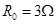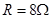，，.闭合开关S，电路稳定后，一带负电的粒子从B板左端且非常靠近B板的位置以初速度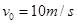水平向右射入，并恰好从A板右边缘飞出。已知粒子的电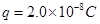量，质量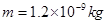（不计空气阻力和粒子重力）。求：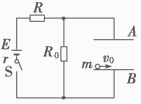

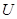（1）两极板间的电势差； （2）电源的内阻.

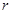违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网