题目内容
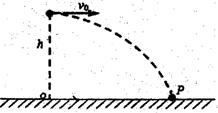
如图所示，竖直放置的半径R=0.4m的半圆形光滑轨道BCD跟水平直轨道AB相切于B点，D点为半圆形轨道的最高点。可视为质点的物块m=0.5kg，静止在水平轨道上A点，物块与轨道AB间的动摩擦因数为μ=0.2，AB两点间的距离为l=2m。现给物块m施以水平向右恒力F作用s="1m" 后撤除恒力，物块滑上圆轨道D点时对轨道压力大小等于物块重力。（g取10m/s2）
（1）求物块m到达B点时的速度大小
（2）求物块落到轨道上距B点的距离x
（3）求恒力F的大小
（1）
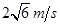（2）
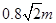（3）8N
解析试题分析：（1）以物块为研究对象，根据题设及牛顿第三定律知物块滑上圆轨道D点时，轨道对物块弹力大小等于物块重力，即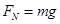
设物块到达D点时的速度为vD，应用牛顿第二定律得：
， 代入数据解得：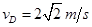
从B到D点过程，只有重做功，机械能守恒：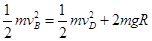
代入数据解得：
（2）物块过D点后做平抛运动，设从D点到落到水平轨道上所需时间为t，根据运动学规律得：
在竖直方向上：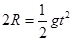
，解得：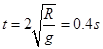
在水平方向上：
（3）物块在AB段：水平向右恒力F做正功，摩擦力做负功．由动能定理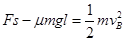得：
解得：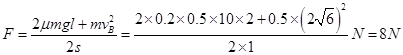
考点：动能定理的应用、牛顿第二定律、平抛运动、机械能守恒定律．
练习册系列答案
相关题目
=37o，其长度为L=26．25m，d点与水平地面间的高度差为h=0．2m，取重力加速度g=10m/s2，sin37°=0．6。求：
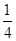圆周轨道，半径OA处于水平位置，CDO是直径为15m的半圆轨道，两个轨道如图连接固定。一个小球P从A点的正上方距水平半径OA高H处自由落下，沿竖直平面内的轨道运动。通过CDO轨道的最低点C时对轨道的压力力等于其重力的
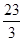倍.取g为10m/s2.
的电动机上，装有质量为
的偏心轮，偏心轮的重心
距转轴的距离为
.当偏心轮重心在转轴
正上方时，电动机对地面的压力刚好为零.求电动机转动的角速度
.
和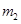
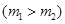，电荷量均为
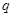.加速电场的电势差为
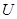，离子进入电场时的初速度可以忽略.不计重力，也不考虑离子间的相互作用。
；
.
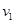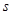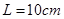，两板间的距离
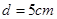.电源的电动势
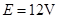，内阻未知，
，
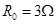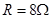.闭合开关S，电路稳定后，一带负电的粒子从B板左端且非常靠近B板的位置以初速度
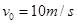水平向右射入，并恰好从A板右边缘飞出。已知粒子的电量
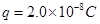，质量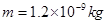
（不计空气阻力和粒子重力）。求：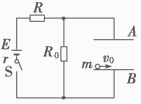
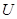； （2）电源的内阻
.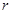