题目内容
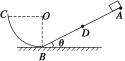
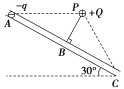
【题目】在直角坐标系xoy中,A(-0.3,0)、C是x轴上两点,P点的坐标为(0,0.3)。在第二象限内以D(-0.3,0.3)为圆心、0.3m为半径的1/4圆形区域内,分布着方向垂直xoy平面向外、磁感应强度大小为B=0.1T的匀强磁场;在第一象限三角形OPC之外的区域,分布着沿y轴负方向的匀强电场(如图所示)。现有大量质量为![]() kg、电荷量为
kg、电荷量为![]() C的相同粒子,从A点平行xoy平面以相同速率
C的相同粒子,从A点平行xoy平面以相同速率![]() m/s沿不同方向射向磁场区域,其中沿AD方向射入的粒子恰好从P点垂直y轴进入电场,恰好通过C点。已知α = 37°,不考虑粒子间的相互作用及其重力,求:
m/s沿不同方向射向磁场区域,其中沿AD方向射入的粒子恰好从P点垂直y轴进入电场,恰好通过C点。已知α = 37°,不考虑粒子间的相互作用及其重力,求:
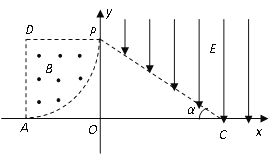
(1)电场强度E的大小;
(2)粒子穿越x正半轴的最大值。
【答案】(1)![]() (2)0.5m
(2)0.5m
【解析】
(1)带电粒子在磁场中做匀速圆周运动,设半径为r,粒子的初速度为v
![]()
![]()
根据题意和几何知识,可得:r=DP=0.3m v=1×103m/s
沿AD方向的粒子由P点进入电场时,速度方向与y轴垂直。所以,该粒子在电场中做类平抛运动,运动时间为t
OC=vt
OP=![]() at2
at2
OP=OCtanα
qE=ma
E=112.5V/m
(2)若速度方向与x轴正方向的夹角为θ的入射粒子,从x正半轴穿过时距离O点最远。
粒子从F点离开磁场,其中![]() 是粒子运动的圆心。由于粒子的运动半径等于磁场的半径,所以四边形
是粒子运动的圆心。由于粒子的运动半径等于磁场的半径,所以四边形![]() 为菱形,
为菱形,![]() ,
,![]() ,而AD又是竖直方向,所以vF垂直于y轴从
,而AD又是竖直方向,所以vF垂直于y轴从![]() 点进入电场,仍做类平抛运动。
点进入电场,仍做类平抛运动。
运动时间为![]()
![]()
![]()
粒子到达x轴的坐标为![]()
![]()
![]()
![]()
联合接的![]()
设![]() ,所以
,所以![]() 当k=0.5时
当k=0.5时![]() 有最大值且为0.5m.
有最大值且为0.5m.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目