题目内容
【题目】一质量为M=2．0kg的小物块随足够长的水平传送带一起运动，被一水平向左飞来的子弹击中并从物块中穿过，子弹和小物块作用时间极短，如图所示，地面观察着记录了小物块被击中后的速度随时间的变化关系，如图所示（图中取向右运动的方向为正方向），已知传送带的速度保持不变，g取10m/s2
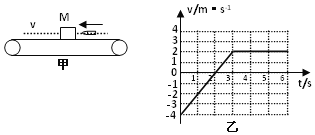
（1）指出传送带速度v的大小和方向；
（2）计算物块与传送带间的动摩擦系数μ？
（3）计算在物块与传送带相对滑动过程系统有多少能量转化为内能？
【答案】（1）向右的2m/s；（2）0．2（3）36．0（J）
【解析】
试题分析：（1）由速度时间图像可知，物块被击穿后，先向左减速运动，速度为零后，又向右加速运动，当速度为2m/s时，随传送带一起匀速运动，故传送带的速度为向右的2m/s；
（2）由速度图象可得，物块在滑动摩擦力的作用下做匀变速运动的加速度为：
．
由牛顿第二定律得：滑动摩擦力 f=Ma
其中 f=μFN=μMg
得到物块与传送带间的动摩擦因数
（3）物块相对传送带通过的路程为：s′=S物+S皮=
（v0-v）t1+vt=
×（4-2）×3+2×3=9（m）
所以产生的内能 EQ=μMgs′=0．2×2×10×9=36．0（J）
练习册系列答案
相关题目
