题目内容
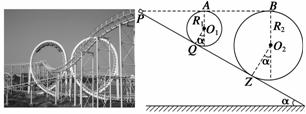
 如图所示,是游乐场翻滚过山车示意图,斜面轨道AC,弯曲、水平轨道CDE和半径R=7.5m的竖直圆形轨道平滑连接.质量m=100kg的实验小车,从距水平面H=20m高处的A点静止释放,通过最低点C后沿圆形轨道运动一周后进入弯曲、水平轨道CDE.重力加速度g=10m/s2,AC与水平面的倾角θ=37°,小车与AC的摩擦因数μ=0.3,其余不计摩擦和阻力.(sin37°=0.6,cos37°=0.8)求:
如图所示,是游乐场翻滚过山车示意图,斜面轨道AC,弯曲、水平轨道CDE和半径R=7.5m的竖直圆形轨道平滑连接.质量m=100kg的实验小车,从距水平面H=20m高处的A点静止释放,通过最低点C后沿圆形轨道运动一周后进入弯曲、水平轨道CDE.重力加速度g=10m/s2,AC与水平面的倾角θ=37°,小车与AC的摩擦因数μ=0.3,其余不计摩擦和阻力.(sin37°=0.6,cos37°=0.8)求:(1)小车从A点静止释放到达圆形轨道最低点C时,轨道对小车支持力的大小
(2)计算说明小车能不能通过圆形轨道最高点B;
(3)为使小车在运动中不脱离圆形轨道,小车初始下落高度H值的范围.
分析:(1)由动能定理求出小车到达C点时的速度,然后由牛顿第二定律求出轨道对C的支持力;
(2)小车经过B点时轨道对它的支持力恰好为零时的速度是小车经过最高点的最小速度,由牛顿第二定律求出该速度,然后由动能定理求出小车到达B点的速度,然后判断小车能否经过B点;
(3)由动能定理求出小车释放的高度.
(2)小车经过B点时轨道对它的支持力恰好为零时的速度是小车经过最高点的最小速度,由牛顿第二定律求出该速度,然后由动能定理求出小车到达B点的速度,然后判断小车能否经过B点;
(3)由动能定理求出小车释放的高度.
解答:解:(1)由动能定理得:mgH-μmgcos37°?
=
mvC2-0,
由牛顿第二定律可得:F-mg=m
,
联立解得:F=1320N;
(2)小车恰好通过B点时,由牛顿第二定律得:
mg=m
,
解得:vBmin=
=
=5
m/s,
从A点到B点,mgH-μmgcos37°?
-mg?2R<0,
则小车不能到达B点;
(3)设小车恰好到达B点时,释放点的高度为H′,
则mgH′-μmgcos37°?
-mg?2R=
mvBmin2-0,
解得:H′=87.5m;
小车恰好到达与圆心同高位置的释放点高度设为h,
则由动能定理得:mgh-μmgcos37°?
-mgR=0-0,
解得:h=12.5m;
则小车不脱离圆形轨道需要满足的条件是:H≥87.5m或0<H<12.5m;
答:(1)轨道对小车支持力的大小为1320N;
(2)小车不能通过圆形轨道最高点B;
(3)为使小车在运动中不脱离圆形轨道,小车初始下落高度H值的范围是:H≥87.5m或0<H<12.5m.
| H |
| sin37° |
| 1 |
| 2 |
由牛顿第二定律可得:F-mg=m
| ||
| R |
联立解得:F=1320N;
(2)小车恰好通过B点时,由牛顿第二定律得:
mg=m
| ||
| R |
解得:vBmin=
| gR |
| 10×7.5 |
| 3 |
从A点到B点,mgH-μmgcos37°?
| H |
| sin37° |
则小车不能到达B点;
(3)设小车恰好到达B点时,释放点的高度为H′,
则mgH′-μmgcos37°?
| H′ |
| sin37° |
| 1 |
| 2 |
解得:H′=87.5m;
小车恰好到达与圆心同高位置的释放点高度设为h,
则由动能定理得:mgh-μmgcos37°?
| h |
| sin37° |
解得:h=12.5m;
则小车不脱离圆形轨道需要满足的条件是:H≥87.5m或0<H<12.5m;
答:(1)轨道对小车支持力的大小为1320N;
(2)小车不能通过圆形轨道最高点B;
(3)为使小车在运动中不脱离圆形轨道,小车初始下落高度H值的范围是:H≥87.5m或0<H<12.5m.
点评:分析清楚小车的运动过程,应用动能定理、牛顿第二定律即可正确解题.

练习册系列答案
相关题目